练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】点E（a,b）到x轴的距离是4，到y轴距离是3，则有（ ）
    A.a=3，b=4
    B.a=±3,b=±4
    C.a=4，b=3
    D.a=±4,b=±3

    【答案】B
    【解析】

    要根据两个条件解答：
    ①点到y轴的距离为3，即横坐标为±3；
    ②点到x轴的距离为4，即纵坐标为±4．

    ∵点E到x轴的距离是4，点P到y轴的距离是3，
    ∴点E的横坐标的绝对值是：3，纵坐标的绝对值是：4，
    ∴|a|=3，|b|=4，
    ∴a=±3，b=±4，
    故选：B，

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】我们规定一种新运算“★”，其意义为a★b=a2-ab-5,如2★1=22-2×1-5=-3.则（-4）★（-2）的值为（ ）

    A. 3 B. -3 C. -13 D. -29

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形ABCD中，E、F分别是边BC、CD上的点， =，CF=DF，连接AE、AF、EF，并延长FE交AB的延长线于点G．

    （1）若正方形的边长为4，则EG等于 ；

    （2）求证：△ECF∽△FDA；

    （3）比较∠EAB与∠EAF的大小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若x3m﹣2﹣2yn﹣1=3是二元一次方程，则m= ， n=

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一组数据：3，2，1，2，2，3，则这组数据的众数是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】中国古代数学家杨辉的《田亩比类乘除捷法》有这么一道题：“直田积八百六十四步，只云长阔共六十步，问长多阔几何？”意思是：一块矩形田地的面积为864平方步，只知道它的长与宽共60步，问它的长比宽多多少步？经过计算，你的结论是：长比宽多（ ）
    A.12步
    B.24步
    C.36步
    D.48步

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知点P在第三象限,且到x轴的距离为3,到y轴的距离为5,则点P的坐标为（ ）

    A.(3,5)
    B.(-5,3)
    C.(3,-5)
    D.(-5,-3)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】【问题情境】

    课外兴趣小组活动时，老师提出了如下问题：

    如图①，△ABC中，若AB＝12，AC＝8，求BC边上的中线AD的取值范围．

    小明在组内经过合作交流，得到了如下的解决方法：延长AD至点E，使DE＝AD，连接BE．请根据小明的方法思考：

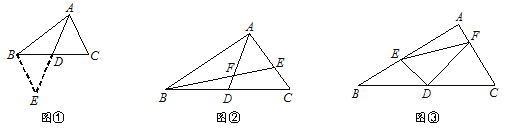
    （1）由已知和作图能得到△ADC≌△EDB，依据是 ．

    A．SSS B．SAS C．AAS D．HL

    （2）由“三角形的三边关系”可求得AD的取值范围是 ．

    解后反思：题目中出现“中点”、“中线”等条件，可考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集中到同一个三角形之中．

    【初步运用】

    如图②，AD是△ABC的中线，BE交AC于E，交AD于F，且AE＝EF．若EF＝3，EC＝2，求线段BF的长．

    【灵活运用】

    如图③，在△ABC中， ∠A＝90°，D为BC中点， DE⊥DF，DE交AB于点E，DF交AC于点F，连接EF．试猜想线段BE、CF、EF三者之间的等量关系，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于x的一元二次方程2x2﹣3kx+4=0的一个根是1，则k= ．

    查看答案和解析>>

    同步练习册答案