Question

△ABC为不等边三角形．∠A及其外角平分线分别交对边中垂线于A₁，A₂，同样得到B₁，B₂，C₁，C₂．求证：A₁A₂=B₁B₂=C₁C₂．

Answer 1

分析：作辅助线连接A₁B，A₁C，过A₁做A₁F⊥AC于F，A₁E⊥AB于E，得到∠ABA₁+∠ACA₁=180°，进一步推出A、B、A₁、C四点共圆，A、A₂、B、C四点共圆，即A₁、A₂都在△ABC的外接圆上，推出∴A₁A₂是△ABC的外接圆的直径，B₁B₂、C₁C₂也是ABC的外接圆的直径，即可得出答案．

解答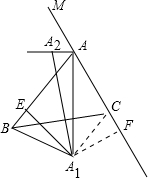：证明：连接A₁B，A₁C，过A₁做A₁F⊥AC于F，A₁E⊥AB于E，
∵连接A₁B、A₁C，
∵AA₁平分∠BAC，
∴A₁E=A₁F，
∵A₁在BC的中垂线上，
∴A₁B=A₁C，
∵∠BEA₁=∠CFA₁=90°，
∴Rt△A₁EB～Rt△A₁FC，
∴∠ABA₁=∠A₁CF，
∵∠A₁CF+∠ACA₁=180°，
∴∠ABA₁+∠ACA₁=180°，
∴A、B、A₁、C四点共圆，
同理A、A₂、B、C四点共圆，
从而知A₁、A₂都在△ABC的外接圆上，
∵AA₁平分∠BAC，AA₂平分∠MAB，
∴∠A₂AA₁=

1

2

×180°=90°，
∴A₁A₂是△ABC的外接圆的直径，
同理可证：B₁B₂、C₁C₂也是ABC的外接圆的直径，
∴A₁A₂=B₁B₂=C₁C₂．

点评：本题主要考查了四点共圆，三角形的外接圆与外心，圆周角定理，确定圆的条件，三角形的角平分线等知识点，通过作辅助线得到A₁、A₂都在△ABC的外接圆上是解此题的关键．