
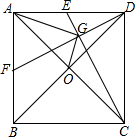
 已知如图,正方形ABCD的对角线AC、BD交于O,点E、F分别是AD、AB边的中点,连接DF、CE交于点G,连接AG、OG.若AD=2,则OG=$\frac{\sqrt{10}}{5}$.
已知如图,正方形ABCD的对角线AC、BD交于O,点E、F分别是AD、AB边的中点,连接DF、CE交于点G,连接AG、OG.若AD=2,则OG=$\frac{\sqrt{10}}{5}$. 分析 作AM⊥DF垂足为M,连接BM,作MH⊥AB于H.首先利用△ADF≌△DCE推出∠EGD=90°,由AM∥EG,AE=ED推出MG=GD,因为OB=OD,所以OG=$\frac{1}{2}$BM,只要求出HM,HB即可解决问题.
解答 解:作AM⊥DF垂足为M,连接BM,作MH⊥AB于H.
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠DAB=∠ADC=90°,OB=OD,
∵AF=FB,AE=ED,
∴AF=FB=AE=ED,
在△ADF和△DCE中,
$\left\{\begin{array}{l}{DA=DC}\\{∠DAF=∠EDC}\\{AF=DE}\end{array}\right.$,
∴△ADF≌△DCE,
∴∠ADF=∠ECD,
∵∠ECD+∠DEC=90°,
∴∠DEC+∠EDF=90°,
∴∠EGD=90°,
∵∠AMD=∠EGD=90°,
∴AM∥EG,
∵AE=ED,
∴MG=GD
∵BO=OD,
∴OG=$\frac{1}{2}$BM.
在RT△ADF中,∵∠DAF=90°,AD=2,AF=1,
∴DF=$\sqrt{5}$,AM=$\frac{AF•AD}{DF}$=$\frac{2\sqrt{5}}{5}$,
在RT△AMF中,∵∠AMF=90°,AF=1,AM=$\frac{2\sqrt{5}}{5}$,
∴FM=$\sqrt{A{F}^{2}-A{M}^{2}}$=$\frac{\sqrt{5}}{5}$,MH=$\frac{AM•MF}{AF}$=$\frac{2}{5}$,
∴AH=$\sqrt{A{M}^{2}-M{H}^{2}}$=$\frac{4}{5}$,HF=$\frac{1}{5}$,BH=$\frac{6}{5}$,
∴BM=$\sqrt{H{M}^{2}+B{H}^{2}}$=$\sqrt{(\frac{6}{5})^{2}+(\frac{2}{5})^{2}}$=$\frac{2\sqrt{10}}{5}$,
∴OG=$\frac{1}{2}$BM=$\frac{\sqrt{10}}{5}$.
故答案为$\frac{\sqrt{10}}{5}$.
点评 本题考查正方形的性质、全等三角形的判定和性质、三角形中位线定理勾股定理等知识,解题的关键是添加辅助线,利用三角形中位线解决问题,所以中考常考题型.


科目:初中数学 来源: 题型:填空题
 如图,点E为正方形ABCD中AD边上的动点,AB=2,以BE为边画正方形BEFG,连结CF和CE,则△CEF面积的最小值为$\frac{3}{2}$.
如图,点E为正方形ABCD中AD边上的动点,AB=2,以BE为边画正方形BEFG,连结CF和CE,则△CEF面积的最小值为$\frac{3}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
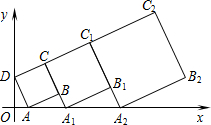 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作第1个正方形A1B1C1C;延长C1B1交x轴于点A2,作第2个正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积是5×($\frac{3}{2}$)4030.
在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作第1个正方形A1B1C1C;延长C1B1交x轴于点A2,作第2个正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积是5×($\frac{3}{2}$)4030.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=ax2+bx+c经过点A(-3,0)、B(1,0)、C(0,3).
如图,抛物线y=ax2+bx+c经过点A(-3,0)、B(1,0)、C(0,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
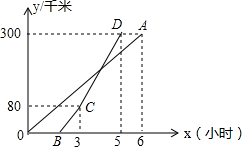 甲乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地如图、线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与时间x(小时)之间的函数关系,根据图象解答下列问题:
甲乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地如图、线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与时间x(小时)之间的函数关系,根据图象解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知∠BAC=90°,四边形ADEF是正方形且边长为1,则$\frac{1}{AB}$+$\frac{1}{BC}$+$\frac{1}{CA}$的最大值为1+$\frac{\sqrt{2}}{4}$,简述理由(可列式):$\frac{1}{AB}$+$\frac{1}{BC}$+$\frac{1}{CA}$的最大值=1+$\frac{\sqrt{2}}{4}$.
已知∠BAC=90°,四边形ADEF是正方形且边长为1,则$\frac{1}{AB}$+$\frac{1}{BC}$+$\frac{1}{CA}$的最大值为1+$\frac{\sqrt{2}}{4}$,简述理由(可列式):$\frac{1}{AB}$+$\frac{1}{BC}$+$\frac{1}{CA}$的最大值=1+$\frac{\sqrt{2}}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
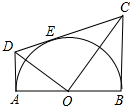 如图,AB为半圆O的直径,CD切⊙O于点E,AD、BC分别切⊙O于A、B两点,AD与CD相交于D,BC与CD相交于C,连接OD、OC,对于下列结论:①OD2=DE•CD;②AD+BC=CD;③OD=OC;④S梯形ABCD=CD•OA;⑤∠DOC=90°;⑥若切点E在半圆上运动(A、B两点除外),则线段AD与BC的积为定值.其中正确的个数是( )
如图,AB为半圆O的直径,CD切⊙O于点E,AD、BC分别切⊙O于A、B两点,AD与CD相交于D,BC与CD相交于C,连接OD、OC,对于下列结论:①OD2=DE•CD;②AD+BC=CD;③OD=OC;④S梯形ABCD=CD•OA;⑤∠DOC=90°;⑥若切点E在半圆上运动(A、B两点除外),则线段AD与BC的积为定值.其中正确的个数是( )| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com