
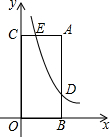
 已知,如图,点A($\sqrt{3}$,3),AB⊥x轴于点B,AC⊥y轴于点C,反比例函数y=$\frac{k}{x}$(x>0)的图象与线段AB、AC分别交于D、E.若AB=3BD,则点E的横坐标为$\frac{\sqrt{3}}{3}$.
已知,如图,点A($\sqrt{3}$,3),AB⊥x轴于点B,AC⊥y轴于点C,反比例函数y=$\frac{k}{x}$(x>0)的图象与线段AB、AC分别交于D、E.若AB=3BD,则点E的横坐标为$\frac{\sqrt{3}}{3}$. 分析 求出AB,求出BD,求出D的坐标,代入函数解析式求出函数解析式,把y=3代入即可求出点E的横坐标.
解答 解:∵点A($\sqrt{3}$,3),AB⊥x轴于点B,AC⊥y轴于点C,
∴AB=3,OB=$\sqrt{3}$,
∵AB=3BD,
∴BD=1,
即D点的坐标为($\sqrt{3}$,1),
∵点D在函数y=$\frac{k}{x}$(x>0)上,
∴k=$\sqrt{3}$×1=$\sqrt{3}$,
即y=$\frac{\sqrt{3}}{x}$,
把y=3代入y=$\frac{\sqrt{3}}{x}$得:x=$\frac{\sqrt{3}}{3}$,
故答案为:$\frac{\sqrt{3}}{3}$.
点评 本题考查了反比例函数图象上点的坐标特征,用待定系数法求函数的解析式的应用,能求出反比例函数的解析式是解此题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 为了解某中学800名学生的视力情况,从中随机抽取了50名学生进行调查,在此调查中,样本容量为50名学生的视力 | |
| B. | 若一个游戏的中奖率是1%,则做100次这样的游戏一定会中奖 | |
| C. | 了解无锡市每天的流动人口数,采用抽查方式 | |
| D. | “掷一枚硬币,正面朝上”是必然事件 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售量n(件) | n=50-x |
| 销售单价m(元/件) | 当1≤x≤20时,m=20+$\frac{1}{2}$x |
| 当21≤x≤30时,m=10+$\frac{420}{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
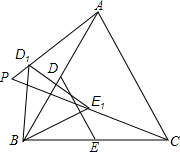 已知:在等边△ABC中,AB=2$\sqrt{3}$,D、E分别是AB,BC的中点(如图),若将△BDE绕点B逆时针旋转,得到△BD1E1.设旋转的角为α(0°<α<180°),记射线CE1与AD1的交点为P,点P到BC所在直线的距离的最大值为2.
已知:在等边△ABC中,AB=2$\sqrt{3}$,D、E分别是AB,BC的中点(如图),若将△BDE绕点B逆时针旋转,得到△BD1E1.设旋转的角为α(0°<α<180°),记射线CE1与AD1的交点为P,点P到BC所在直线的距离的最大值为2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
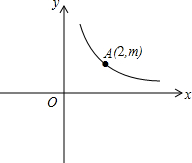 在平面直角坐标系xOy中,反比例函数y=$\frac{k}{x}$(k>0)的图象经过点A(2,m),连接OA,在x轴上有一点B,且AO=AB,△AOB的面积为2.
在平面直角坐标系xOy中,反比例函数y=$\frac{k}{x}$(k>0)的图象经过点A(2,m),连接OA,在x轴上有一点B,且AO=AB,△AOB的面积为2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com