
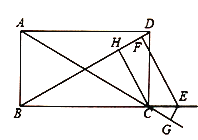
【题目】如图1,⊙O的直径AB=12,P是弦BC上一动点(与点B,C不重合),∠ABC=30°,过点P作PD⊥OP交⊙O于点D.
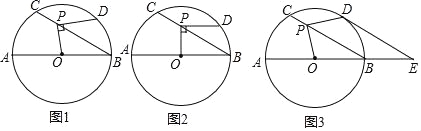
(1)如图2,当PD∥AB时,求PD的长;
(2)如图3,当![]() 时,延长AB至点E,使BE=
时,延长AB至点E,使BE=![]() AB,连接DE.
AB,连接DE.
①求证:DE是⊙O的切线;
②求PC的长.
【答案】(1)![]() (2)①证明见解析②3
(2)①证明见解析②3![]() ﹣3
﹣3
【解析】
试题分析:(1)根据题意首先得出半径长,再利用锐角三角三角函数关系得出OP,PD的长;
(2)①首先得出△OBD是等边三角形,进而得出∠ODE=∠OFB=90°,求出答案即可;
②首先求出CF的长,进而利用直角三角形的性质得出PF的长,进而得出答案.
试题解析:(1)如图2,连接OD,
∵OP⊥PD,PD∥AB,
∴∠POB=90°,
∵⊙O的直径AB=12,
∴OB=OD=6,
在Rt△POB中,∠ABC=30°,
∴OP=OBtan30°=6×![]() =2
=2![]() ,
,
在Rt△POD中,
PD=![]() =
=![]() =
=![]() ;
;
(2)①如图3,连接OD,交CB于点F,连接BD,
∵![]() ,
,
∴∠DBC=∠ABC=30°,
∴∠ABD=60°,
∵OB=OD,
∴△OBD是等边三角形,
∴OD⊥FB,
∵BE=![]() AB,
AB,
∴OB=BE,
∴BF∥ED,
∴∠ODE=∠OFB=90°,
∴DE是⊙O的切线;
②由①知,OD⊥BC,
∴CF=FB=OBcos30°=6×![]() =3
=3![]() ,
,
在Rt△POD中,OF=DF,
∴PF=![]() DO=3(直角三角形斜边上的中线,等于斜边的一半),
DO=3(直角三角形斜边上的中线,等于斜边的一半),
∴CP=CF﹣PF=3![]() ﹣3.
﹣3.


科目:初中数学 来源: 题型:
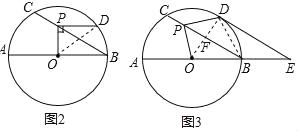
【题目】如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,BE=AF.
(1)求证:四边形ADEF是平行四边形;
(2)若∠ABC=60°,BD=4,求平行四边形ADEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
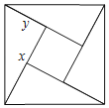
【题目】如图,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案.已知大正方形面积为49,小正方形面积为4,若用![]() ,
,![]() 表示直角三角形的两直角边
表示直角三角形的两直角边![]() ,下列四个说法:①
,下列四个说法:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;其中说法正确的是
;其中说法正确的是![]()
![]()
A. ①②B. ①②③C. ①②④D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OC在∠BOD内.
(1)如果∠AOC和∠BOD都是直角.
①若∠BOC=60°,则∠AOD的度数是 ;
②猜想∠BOC与∠AOD的数量关系,并说明理由;
(2)如果∠AOC=∠BOD=x°,∠AOD=y°,求∠BOC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知线段 AB=12cm,点 C 为 AB 上的一个动点,点 D,E 分别是 AC 和 BC的中点.
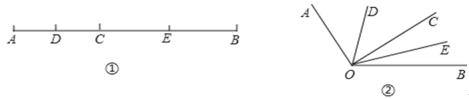
(1)若 AC=4cm,求 DE 的长.
(2)若 AC=acm(不超过 12cm),求 DE 的长.
(3)知识迁移:如图②,已知∠AOB=120°,过角的内部任意一点 C 画射线OC,若OD,OE 分别平分∠AOC 和∠BOC,求∠DOE 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
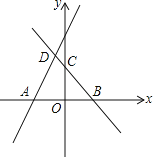
【题目】如图,直线y=![]() x+m与x轴交于点A(-3,0),直线y=-x+2与x轴、y轴分别交于B、C两点,并与直线y=
x+m与x轴交于点A(-3,0),直线y=-x+2与x轴、y轴分别交于B、C两点,并与直线y=![]() x+m相交于点D,
x+m相交于点D,
(1)点D的坐标为 ;
(2)求四边形AOCD的面积;
(3)若点P为x轴上一动点,当PD+PC的值最小时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对于一个数x,我们把[x]称作x的相伴数;若x≥0,则[x]=x﹣1;若x<0,则[x]=x+1.例:[0.5]=﹣0.5.
(1)求[![]() ]、[﹣1]的值;
]、[﹣1]的值;
(2)当a>0,b<0时,有[a]=[b],试求代数式(b﹣a)3﹣3a+3b的值;
(3)解方程:[x]+[x+2]=1.
查看答案和解析>>
科目:初中数学 来源: 题型:
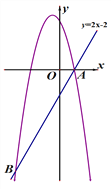
【题目】已知直线y=2x-2与抛物线![]() 交于点A(1,0)和点B,且m<n.
交于点A(1,0)和点B,且m<n.
(1)当m=![]() 时,直接写出该抛物线顶点的坐标.
时,直接写出该抛物线顶点的坐标.
(2)求点B的坐标(用含m的代数式表示).
(3)设抛物线顶点为C,记△ABC的面积为S.
①![]() ,求线段AB长度的取值范围;
,求线段AB长度的取值范围;
②当![]() 时,求对应的抛物线的函数表达式
时,求对应的抛物线的函数表达式
查看答案和解析>>
科目:初中数学 来源: 题型:
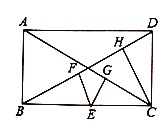
【题目】(1)如图,已知矩形![]() 中,点
中,点![]() 是边
是边![]() 上的一动点(不与点
上的一动点(不与点![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,猜想线段
,猜想线段![]() 三者之间具有怎样的数量关系,并证明你的猜想;
三者之间具有怎样的数量关系,并证明你的猜想;
(2)如图,若点![]() 在矩形
在矩形![]() 的边
的边![]() 的延长线上,过点
的延长线上,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,![]() 于点
于点![]() ,则线段
,则线段![]() 三者之间具有怎样的数量关系,直接写出你的结论;
三者之间具有怎样的数量关系,直接写出你的结论;
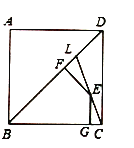
(3)如图,![]() 是正方形
是正方形![]() 的对角线,
的对角线,![]() 在
在![]() 上,且
上,且![]() ,连接
,连接![]() ,点
,点![]() 是
是![]() 上任一点,
上任一点,![]() 与点
与点![]() ,
,![]() 于点
于点![]() ,猜想线段
,猜想线段![]() 之间具有怎样的数量关系,直接写出你的猜想.
之间具有怎样的数量关系,直接写出你的猜想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com