
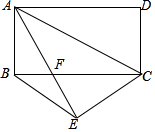
 如图,把矩形ABCD沿AC折叠,点D落在点E处,AE交BC于点F,连接BE,若BE:AC=3:5,求AB:BC的值.
如图,把矩形ABCD沿AC折叠,点D落在点E处,AE交BC于点F,连接BE,若BE:AC=3:5,求AB:BC的值. 分析 证明△ABF≌△CEF,得出AF=CF,BF=EF,证出∠FAC=∠FCA,∠FBE=∠FEB,证明△AFC∽△BFE,得出$\frac{BF}{AF}=\frac{BE}{AC}$=$\frac{3}{5}$,设BF=3x,AF=5x,由勾股定理求出AB=$\sqrt{A{F}^{2}-B{F}^{2}}$=4x,CF=AF=5x,得出BC=8x,即可得出答案.
解答 解:∵∵四边形ABCD是矩形,
∴∠ABF=∠D=90°,AB=CD,
由折叠的性质得:∠CEF=∠D=90°,CE=CD,
∴∠ABF=∠CEF,AB=CE,
在△ABF和△CEF中,$\left\{\begin{array}{l}{∠ABF=∠CEF}&{\;}\\{∠AFB=∠CFE}&{\;}\\{AB=CE}&{\;}\end{array}\right.$,
∴△ABF≌△CEF(AAS),
∴AF=CF,BF=EF,
∴∠FAC=∠FCA,∠FBE=∠FEB,
∵∠AFC=∠BFE,
∴∠FAC=∠FBE,
∴△AFC∽△BFE,
∴$\frac{BF}{AF}=\frac{BE}{AC}$=$\frac{3}{5}$,
设BF=3x,AF=5x,
则AB=$\sqrt{A{F}^{2}-B{F}^{2}}$=4x,CF=AF=5x,
∴BC=3x+5x=8x,
∴$\frac{AB}{BC}$=$\frac{4x}{8x}$=$\frac{1}{2}$.
点评 本题考查了矩形的性质,折叠的性质,等腰三角形的性质,全等三角形的判定与性质,相似三角形的判定与性质,勾股定理的应用,综合性较强,有一定难度.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:解答题
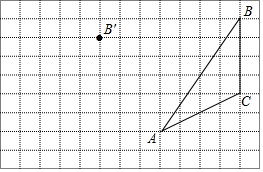 如图,在方格纸内将三角形ABC经过平移后得到三角形A′B′C′,图中标出了点B的对应点B′,解答下列问题.
如图,在方格纸内将三角形ABC经过平移后得到三角形A′B′C′,图中标出了点B的对应点B′,解答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
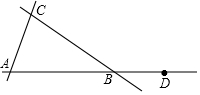 如图,三个村庄A,B,C分别位于三条公路的两两交汇处,形成△ABC,且BA=BC,现计划修建一个粮仓G满足以下两个条件:①在∠CBD的平分线上;②在边BC的中线AF所在的直线上,请用尺规画出粮仓G的位置(不写画法,但要保留作图痕迹,在图中标明相应的字母);BG与边AC的位置关系怎样?
如图,三个村庄A,B,C分别位于三条公路的两两交汇处,形成△ABC,且BA=BC,现计划修建一个粮仓G满足以下两个条件:①在∠CBD的平分线上;②在边BC的中线AF所在的直线上,请用尺规画出粮仓G的位置(不写画法,但要保留作图痕迹,在图中标明相应的字母);BG与边AC的位置关系怎样?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
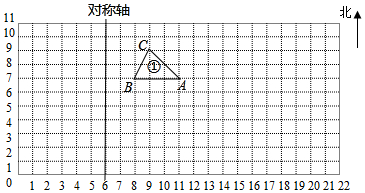 如图每个小正方形的边长表示1厘米,请按要求画图形.
如图每个小正方形的边长表示1厘米,请按要求画图形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
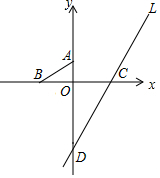 如图,在坐标平面上,O为原点,另有A(0,3),B(-5,0),C(6,0)三点,直线L通过C点且与y轴相交于D点,请回答下列问题:
如图,在坐标平面上,O为原点,另有A(0,3),B(-5,0),C(6,0)三点,直线L通过C点且与y轴相交于D点,请回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
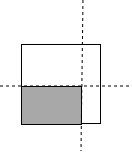 某同学想用一块面积为400cm2的正方形纸片,(如图所示)沿着边的方向裁出一块面积为300cm2的长方形纸片,使它的长宽之比为3:2,请你用所学过的知识来说明能否用这块纸片裁出符合要求的纸片.
某同学想用一块面积为400cm2的正方形纸片,(如图所示)沿着边的方向裁出一块面积为300cm2的长方形纸片,使它的长宽之比为3:2,请你用所学过的知识来说明能否用这块纸片裁出符合要求的纸片.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com