
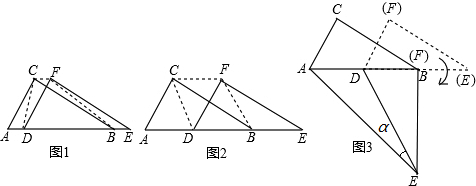
分析 (1)如图1,先利用平移的性质得CF=AD,AC=DF,则可判断四边形ACFD为平行四边形,利用三角形面积公式得到S△DCF=S△BCF=S△ACD,则S四边形CDBF=S△ACB,然后计算S△ABC即可;
(2)如图2,利用直角三角形斜边上的中线性质得DC=DA=DB,则可证明四边形CDBF为平行四边形,于是可判断四边形CDBF为菱形;
(3)作DH⊥AE于H,如图,先计算出AB=2AC=2,则AD=BD=$\frac{1}{2}$AB=1,再利用旋转的性质得∠EFD=90°,EB=$\sqrt{3}$,DE=AB=2,接着利用勾股定理计算出AE=$\sqrt{7}$,然后利用面积法可计算出DH=$\frac{\sqrt{21}}{7}$,再在Rt△EDH中利用正弦的定义求sinα的值.
解答 解:(1)如图1,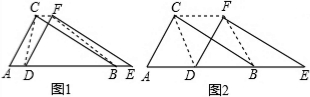
∵△DEF沿线段AB向右平移(即D点在线段AB内移动),
∴CF=AD,AC=DF,
∴四边形ACFD为平行四边形,
∴AD∥CF,
∴S△DCF=S△BCF=S△ACD,
∴S四边形CDBF=S△CDB+S△BCF=S△CDB+S△ACD=S△ACB,
在Rt△ACB中,∵∠A=60°,
∴BC=$\sqrt{3}$AC=$\sqrt{3}$,
∴S△ABC=$\frac{1}{2}$×1×$\sqrt{3}$=$\frac{\sqrt{3}}{2}$,
∴S四边形CDBF=$\frac{\sqrt{3}}{2}$;
(2)四边形CDBF为菱形.理由如下:
如图2,
∵点D为斜边AB的中点,
∴DC=DA=DB,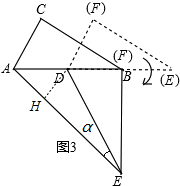
∵CF∥AD,CF=AD,
∴CF=BD,CF∥DB,
∴四边形CDBF为平行四边形,
而DC=DB,
∴四边形CDBF为菱形;
(3)作DH⊥AE于H,如图,
在Rt△ACB中,∵∠A=60°,
∴AB=2AC=2,
∵点D为AB的中点,
∴AD=BD=$\frac{1}{2}$AB=1,
∵绕D点按顺时针方向旋转△DEF,使DF落在AB边上,此时F点恰好与B点重合,
∴∠EFD=90°,EB=$\sqrt{3}$,DE=AB=2,
在Rt△ABE中,AE=$\sqrt{B{E}^{2}+A{B}^{2}}$=$\sqrt{(\sqrt{3})^{2}+{2}^{2}}$=$\sqrt{7}$,
∵$\frac{1}{2}$DH•AB=$\frac{1}{2}$AD•EB,
∴DH=$\frac{1×\sqrt{3}}{\sqrt{7}}$=$\frac{\sqrt{21}}{7}$,
在Rt△EDH中,sinα=$\frac{DH}{DE}$=$\frac{\frac{\sqrt{21}}{7}}{2}$=$\frac{\sqrt{21}}{14}$.
点评 本题考查了几何变换综合题:熟练掌握平移、旋转的性质和菱形的判定方法;理解正弦的定义和运用面积法计算线段的长;记住含30度的直角三角形三边的关系.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
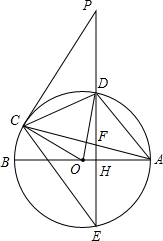 如图,AB、AC分别是⊙O的直径和弦,点D为劣弧AC上一点,弦DE⊥AB分别交⊙O于点D、E,交AB于点H,交AC于点F,P是延长线上一点,且PC=PF.
如图,AB、AC分别是⊙O的直径和弦,点D为劣弧AC上一点,弦DE⊥AB分别交⊙O于点D、E,交AB于点H,交AC于点F,P是延长线上一点,且PC=PF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 北京市在城市建设中,要折除旧烟囱AB,在烟囱正西方向的楼CD的顶端C,测得烟囱的顶端A的仰角为45°,底端B的俯角为30°,已量得DB=21m.拆除时若让烟囱向正东倒下,试问:距离烟囱东方35m远的一棵大树是否被歪倒的烟囱砸着?请说明理由.
北京市在城市建设中,要折除旧烟囱AB,在烟囱正西方向的楼CD的顶端C,测得烟囱的顶端A的仰角为45°,底端B的俯角为30°,已量得DB=21m.拆除时若让烟囱向正东倒下,试问:距离烟囱东方35m远的一棵大树是否被歪倒的烟囱砸着?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x+y)(-y)=x-y2 | B. | x2-3=(x+1)(x-1)-2 | ||
| C. | a2+b2-2ab+1=(a-b)2+1 | D. | x2-4xy+4y2=(x-2y)2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com