

分析 (1)分当F在边AB上时和在AC边上时,两种情况进行讨论,分别利用相似三角形的对应边的比相等求得移动的距离,即可求得时间;
(2)根据(1)得到的时间,即可根据t的范围分三种情形进行讨论,根据相似三角形的性质,以及三角形的面积公式即可得到函数解析式;
(3)存在.分两种情形①如图7中,当D′F′∥BC时,△AGH是等腰三角形.②如图8中,△AGH是等边三角形.分别求解即可.
解答 解:(1)当F在边AB上时,如图(1),作AM⊥BC,
则AM=$\frac{\sqrt{3}}{2}$AB=$\frac{\sqrt{3}}{2}$×6 $\sqrt{3}$=9,
∵AM⊥BC,∠FEB=90°
∴EF∥AM,
∴△BEF∽△BMA,
∴$\frac{BE}{BM}$=$\frac{EF}{AM}$,即 $\frac{BE}{3\sqrt{3}}$=$\frac{6}{9}$,解得:BE=2 $\sqrt{3}$,则移动的距离是:6 $\sqrt{3}$+2 $\sqrt{3}$=8 $\sqrt{3}$,则t=$\frac{8\sqrt{3}}{\sqrt{3}}$=8;
当F在AC上时,如图(2)
同理可得:EC=2 $\sqrt{3}$,则移动的距离是:2×6 $\sqrt{3}$-2 $\sqrt{3}$=12 $\sqrt{3}$-2 $\sqrt{3}$=10 $\sqrt{3}$,则t=$\frac{10\sqrt{3}}{\sqrt{3}}$=10,
故t的值是:8或10;
(2)当0<t≤6时,重合部分是△BND,如图3中,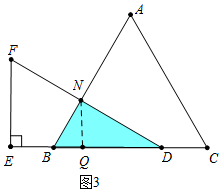
设AB与BE交于点N,
则BD=$\sqrt{3}$t,NB=$\frac{1}{2}$BD=$\frac{\sqrt{3}}{2}$t,ND=$\frac{\sqrt{3}}{2}$BD=$\frac{\sqrt{3}}{2}$×$\sqrt{3}$t=$\frac{3}{2}$t,
S=$\frac{1}{2}$NB•ND=$\frac{1}{2}$×$\frac{\sqrt{3}}{2}$t×$\frac{3}{2}$t=$\frac{3\sqrt{3}}{8}$t2;
当6<t≤8时,重合部分是五边形MNQCE,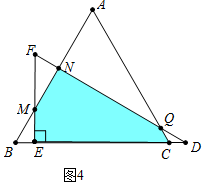
S=S五边形MNQCE-S△MNF-S△CQD=18$\sqrt{3}$-$\frac{1}{2}$•$\frac{1}{2}$•(24-3t)$\frac{\sqrt{3}}{2}$(24-3t)-$\frac{1}{2}$($\sqrt{3}$t-6$\sqrt{3}$)•$\frac{\sqrt{3}}{2}$($\sqrt{3}$t-6$\sqrt{3}$)=-$\frac{15\sqrt{3}}{8}$t2+27$\sqrt{3}$t-81$\sqrt{3}$.
当8<t<10时,重叠部分是四边形EFMC,如图4中,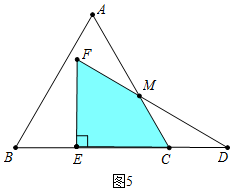
S=S△EDF-S△CDM=18$\sqrt{3}$-$\frac{1}{2}$($\sqrt{3}$t-6$\sqrt{3}$)•$\frac{\sqrt{3}}{2}$($\sqrt{3}$t-6$\sqrt{3}$)=-$\frac{3}{4}$$\sqrt{3}$t2+9$\sqrt{3}$t-9$\sqrt{3}$.
当10≤t<12时,重合部分是△MCE,如图5,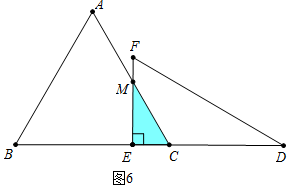
S=$\frac{1}{2}$[6$\sqrt{3}$-($\sqrt{3}$t-6$\sqrt{3}$)]•$\sqrt{3}$•[6$\sqrt{3}$-($\sqrt{3}$t-6$\sqrt{3}$)]=$\frac{3}{2}$$\sqrt{3}$t2-36$\sqrt{3}$t+216$\sqrt{3}$.
综上所述,S=$\left\{\begin{array}{l}{\frac{3\sqrt{3}}{8}{t}^{2}}&{(0<t≤6)}\\{-\frac{15\sqrt{3}}{8}{t}^{2}+27\sqrt{3}t-81\sqrt{3}}&{(6<t≤8)}\\{-\frac{3\sqrt{3}}{4}{t}^{2}+9\sqrt{3}t-9\sqrt{3}}&{(8<t≤10)}\\{\frac{3\sqrt{3}}{2}{t}^{2}-36\sqrt{3}t+216\sqrt{3}}&{(10<t<12)}\end{array}\right.$.
(3)存在.
①如图7中,当D′F′∥BC时,△AGH是等腰三角形.
∵∠GAH=60°,
∴△AGH是等边三角形,
∴∠AGH=∠F′GB=60°=∠F′,
∴△BGF′是等边三角形,
∴BG=BF′=6,
∴AH=AG=AB-BG=6$\sqrt{3}$-6.
②如图8中,△AGH是等边三角形.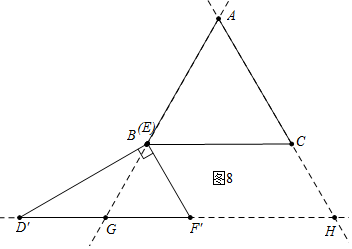
易知△BGF′是等边三角形,
∴BG=BF′=6,
∴AH=AG=AB+BG=6$\sqrt{3}$+6.
综上所述,当△AGH为等腰三角形时AH的长度为6$\sqrt{3}$-6或6$\sqrt{3}$+6.
点评 本题是运三角形综合题、等边三角形的性质.30度的直角三角形的性质、三角形的面积等知识,解题的关键是学会用分类讨论的思考思考问题,学会用分割法求重叠部分面积,属于中考压轴题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在5×4的方格纸中,每个小正方形边长为1,点O、A、B在方格纸的交点(格点)上,在第四象限内的格点上找点C,使△ABC的面积为3,则这样的点C共有个3个.
如图,在5×4的方格纸中,每个小正方形边长为1,点O、A、B在方格纸的交点(格点)上,在第四象限内的格点上找点C,使△ABC的面积为3,则这样的点C共有个3个.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在7×7网格中,每个小正方形的边长都为1.
如图,在7×7网格中,每个小正方形的边长都为1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
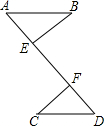 如图所示,已知BE⊥AD,CF⊥AD,垂足分别为E,F,则在下列条件中选择一组,可以判定 Rt△ABE≌Rt△DCF的是①②③(填入序号)
如图所示,已知BE⊥AD,CF⊥AD,垂足分别为E,F,则在下列条件中选择一组,可以判定 Rt△ABE≌Rt△DCF的是①②③(填入序号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com