
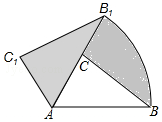
 如图,在△ACB中,∠BAC=60°,AC=2,AB=3,现将△ACB绕点A逆时针旋转60°得到△AC1B1,则阴影部分的面积为$\frac{3}{2}$π.
如图,在△ACB中,∠BAC=60°,AC=2,AB=3,现将△ACB绕点A逆时针旋转60°得到△AC1B1,则阴影部分的面积为$\frac{3}{2}$π. 分析 根据旋转的性质可知S△ABC=S${\;}_{△A{B}_{1}{C}_{1}}$,由此可得S阴影=S${\;}_{扇形AB{B}_{1}}$,根据扇形面积公式即可得出结论.
解答 解:∵S△ABC=S${\;}_{△A{B}_{1}{C}_{1}}$,由此可得S阴影=S${\;}_{扇形AB{B}_{1}}$=$\frac{60•π•{3}^{2}}{360}$π=$\frac{3}{2}$π.
故答案为:$\frac{3}{2}$π.
点评 本题考查了旋转的性质以及扇形的面积公式,解题的关键是找出S阴影=S${\;}_{扇形AB{B}_{1}}$.本题属于基础题,难度不大,解决该题型题目时,根据旋转的性质找出阴影部分的面积等于扇形的面积是关键.


科目:初中数学 来源: 题型:选择题
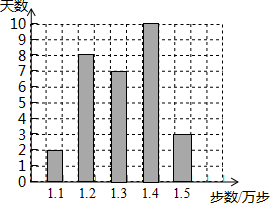 李老师用手机软件记录了上个月(30天)每天走路的步数(单位:万步),她将记录的结果绘制成了如图所示的统计图,关于这组数据的众数是( )
李老师用手机软件记录了上个月(30天)每天走路的步数(单位:万步),她将记录的结果绘制成了如图所示的统计图,关于这组数据的众数是( )| A. | 10 | B. | 1.3 | C. | 1.4 | D. | 1.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
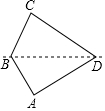 如图,在四边形ABCD中,AB=BC,AD=CD,∠A=∠C=90°,∠B=150°将纸片先沿直线BD对折,再将对折后的图形沿从一个顶点出发的直线裁剪,剪开后的图形打开铺平,若铺平后的图形有一个是面积为8的平行四边形,则CD=4+2$\sqrt{3}$或8+4$\sqrt{3}$.
如图,在四边形ABCD中,AB=BC,AD=CD,∠A=∠C=90°,∠B=150°将纸片先沿直线BD对折,再将对折后的图形沿从一个顶点出发的直线裁剪,剪开后的图形打开铺平,若铺平后的图形有一个是面积为8的平行四边形,则CD=4+2$\sqrt{3}$或8+4$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. | 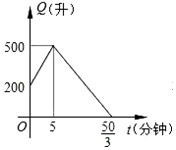 | ||
| C. | 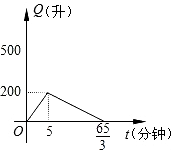 | D. | 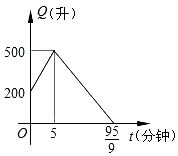 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com