
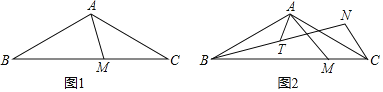
【题目】在△ABC中,AB=AC,∠BAC=120°,M为BC边上一动点(M不与B、C重合)
(1)如图1,若∠MAC=45°,求![]() ;
;
(2)如图2,将CM绕点C顺时针旋转60°至CN,连接BN,T为BN的中点,连接AT.
①求证:AM=2AT;
②当AB=AC=2时,直接写出CM+4AT的最小值为 .
【答案】(1)![]() ;(2)①见解析;②2
;(2)①见解析;②2![]()
【解析】
(1)如图1,过点M作MH⊥AC于H,证△AMH是等腰直角三角形,设AH=a,则MH=a,在Rt△CMH中,求出CH,CM的长,再证BM=AC即可求出结果;
(2)①如图2﹣1,延长BA至Q且使AQ=AB,连接CQ,MN,AN,NQ,证△ACQ和△MCN为等边三角形,推出AN=QN=AM,由三角形的中位线定理即可推出结论;
②如图2﹣2,将△QCN绕点C顺时针旋转60°得到△Q'CN',连接NN',MN,QQ',AQ',设AQ'与QC交于点G,推出CM+4AT=CN+AN+NQ=NN'+AN+N'Q',即当A,N,N',Q'在一条直线上时,CM+4AT有最小值,为AQ'的长度,求出AQ'的长度即可.
(1)解:如图1,过点M作MH⊥AC于H,
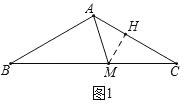
∵∠MAC=45°,
∴△AMH是等腰直角三角形,
设AH=a,则MH=a,
∵AB=AC,∠BAC=120°,
∴∠C=30°,
∴在Rt△CMH中,
CH=![]() MH=
MH=![]() ,CM=2MH=2a,
,CM=2MH=2a,
∴AC=AH+CH=(1+![]() )a,
)a,
∵∠BAM=∠BAC﹣∠CAM=75°,∠BMA=∠C+∠CAM=75°,
∴∠BAM=∠BMA,
∴BM=AB=AC=(1+![]() )a,
)a,
∴![]() ;
;
(2)①证明:如图2﹣1,延长BA至Q且使AQ=AB,连接CQ,MN,AN,NQ
则AC=AQ,
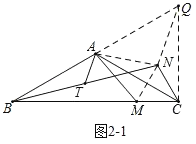
∵∠CAQ=180°﹣∠BAC=60°,
∴△ACQ为等边三角形,
∵CM=CN,∠MCN=60°,
∴△MCN为等边三角形,
∵∠ACM=30°,
∴∠ACN=60°﹣∠ACM=30°,∠QCN=60°﹣∠ACN=30°,
∴AC垂直平分MN,
∵AM=AN,
又∵AC=QC,∠ACN=∠QCN,CN=CN,
∴△ACN≌△QCN(SAS),
∴AN=QN,
∴AM=QN,
∵BA=QA,BT=NT,
∴QN=2AT,
即AM=2AT;
②解:如图2﹣2,将△QCN绕点C顺时针旋转60°得到△Q'CN',连接NN',MN,QQ',AQ',设AQ'与QC交于点G,
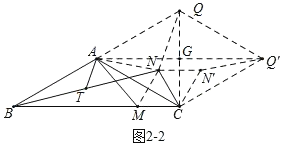
则∠NCN'=∠QCQ'=60°,NQ=N'Q',
又∵CN=CN',CQ=CQ',
∴△CNN'与△CQQ'是等边三角形,
由①知AN=NQ=AM=2AT,
∴CM+4AT=CN+AN+NQ=NN'+AN+N'Q',
即当A,N,N',Q'在一条直线上时,CM+4AT有最小值,为AQ'的长度,
∵△ACQ和△CQQ'是等边三角形,
∴AC=AQ=CQ=QQ'=CQ'=2,
∴四边形ACQ'Q为菱形,
∴AQ'⊥CQ,
∴在Rt△AQG中,
AG=![]() AQ=
AQ=![]() ,
,
∴AQ'=2AG=2![]() ,
,
故答案为:2![]() .
.


科目:初中数学 来源: 题型:
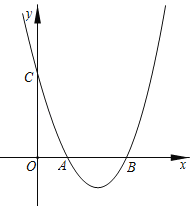
【题目】如图,在平面直角坐标系中,抛物线y=x2+mx+n与x轴正半轴交于A,B两点(点A在点B左侧),与y轴交于点 C.
(1)若△OBC是等腰直角三角形,且其腰长为3,求抛物线的解析式;
(2)在(1)的条件下,点P为抛物线对称轴上的一点,则PA+PC的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家1至6月份的用水量统计如图所示,关于这组数据,下列说法错误的是( ).
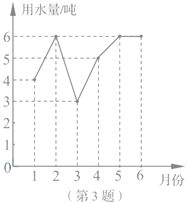
A、众数是6吨 B、平均数是5吨 C、中位数是5吨 D、方差是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市有2000名学生参加了2018年全省八年级数学学业水平测试.其中有这样一题:如图,分别以线段BD的端点B、D为圆心,相同的长为半径画弧,两弧相交于A、C两点,连接AB、AD、CB、CD.若AB=2,BD=2![]() ,求四边形ABCD的面积.
,求四边形ABCD的面积.

统计我市学生解答和得分情况,并制作如下图表:

(1)求学业水平测试中四边形ABCD的面积;
(2)请你补全条形统计图;
(3)我市该题的平均得分为多少?
(4)我市得3分以上的人数为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA、PB、CD是⊙O的切线,A、B、E是切点,CD分别交线段PA、PB于C、D两点,若∠APB=40°,则∠COD的度数为( )
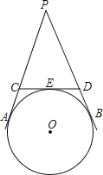
A.50°B.60°C.70°D.75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式及其验证过程:![]() ,验证:
,验证:![]() ,验证:
,验证:![]() .
.
(1)按照上述两个等式及其验证过程,猜想![]() 的变形结果并进行验证;
的变形结果并进行验证;
(2)针对上述各式反映的规律,直接写出用a(a≥2的整数)表示的等式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形![]() 和等腰直角
和等腰直角![]() 中,
中,![]() ,
,![]() 是
是![]() 的中点,连接
的中点,连接![]() 、
、![]() .
.
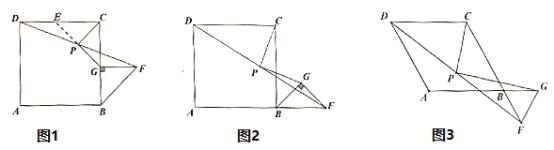
(1)如图1,当点![]() 在
在![]() 边上时,延长
边上时,延长![]() 交
交![]() 于点
于点![]() .求证:
.求证:![]() ;
;
(2)如图2,当点![]() 在
在![]() 的延长线上时,(1)中的结论是否成立?请证明你的结论;
的延长线上时,(1)中的结论是否成立?请证明你的结论;
(3)如图3,若四边形![]() 为菱形,且
为菱形,且![]() ,
,![]() 为等边三角形,点
为等边三角形,点![]() 在
在![]() 的延长线上时,线段
的延长线上时,线段![]() 、
、![]() 又有怎样的数量关系,请直接写出你的结论,并画出论证过程中需要添加的辅助线.
又有怎样的数量关系,请直接写出你的结论,并画出论证过程中需要添加的辅助线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图二次函数的图象与![]() 轴交于点
轴交于点![]() 和
和![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 、
、![]() 是二次函数图象上的一对对称点,一次函数的图象经过
是二次函数图象上的一对对称点,一次函数的图象经过![]() 、
、![]()

(1)求二次函数的解析式;
(2)写出使一次函数值大于二次函数值的![]() 的取值范围;
的取值范围;
(3)若直线![]() 与
与![]() 轴的交点为
轴的交点为![]() 点,连结
点,连结![]() 、
、![]() ,求
,求![]() 的面积;
的面积;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校打算用长![]() 米的篱笆围城一个长方形的生物园饲养小兔,生物园的一面靠在长为
米的篱笆围城一个长方形的生物园饲养小兔,生物园的一面靠在长为![]() 米的墙上(如图).
米的墙上(如图).

(1)若生物园的面积为![]() 平方米,求生物园的长和宽;
平方米,求生物园的长和宽;
(2)能否围城面积为![]() 平方米的生物园?若能,求出长和宽;若不能,请说明理由.
平方米的生物园?若能,求出长和宽;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com