
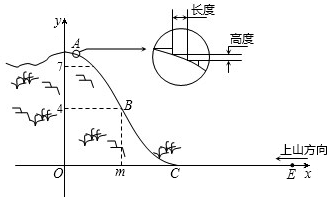
某旅游胜地欲开发一座景观山.从山的侧面进行勘测,迎面山坡线ABC由同一平面内的两段抛物线组成,其中AB所在的抛物线以A为顶点、开口向下,BC所在的抛物线以C为顶点、开口向上.以过山脚(点C)的水平线为x轴、过山顶(点A)的铅垂线为y轴建立平面直角坐标系如图(单位:百米).已知AB所在抛物线的解析式为y=-![]() x2+8,BC所在抛物线的解析式为y=
x2+8,BC所在抛物线的解析式为y=![]() (x-8)2,且已知B(m,4).
(x-8)2,且已知B(m,4).

(1)设P(x,y)是山坡线AB上任意一点,用y表示x,并求点B的坐标;
(2)从山顶开始、沿迎面山坡往山下铺设观景台阶.这种台阶每级的高度为20 cm,长度因坡度的大小而定,但不得小于20 cm,每级台阶的两端点在坡面上(如上图).
①分别求出前三级台阶的长度(精确到1 cm);
②这种台阶不能一起铺到山脚,为什么?(可取点验证)
(3)在山坡上的700 m高度(点D)处恰好有一小块平地,可以用来建造索道站.索道站的起点选择在山脚水平线上的点E处,OE=1 600(m).假设索道DE可近似地看成一段以E为顶点、开口向上的抛物线,解析式为y=![]() (x-16)2.试求索道的最大悬空高度.
(x-16)2.试求索道的最大悬空高度.
|
分析 (1)根据B点的纵坐标可以直接得到其横坐标.(2)从B处能直接铺到山脚,所以只要判断从山顶能否铺到点B.(3)悬空高度实际上是抛物线DE与抛物线BC的函数值的差的最大值. 说明 事实上这种台阶从山顶开始最多只能铺到700 m高度,共500级.从100 m高度到700 m高度都不能铺设这种台阶. (3)D(2,7)、E(16,0)、B(4,4)、C(8,0). 由AB、BC所在抛物线和索道抛物线可知,只有当索道在BC上方时,索道的悬空高度才有可能取最大值.索道在BC上方时,悬空高度y= ∴当x= |


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 28 |
 试求索道的最大悬空高度.
试求索道的最大悬空高度.查看答案和解析>>
科目:初中数学 来源:第6章《二次函数》中考题集(26):6.4 二次函数的应用(解析版) 题型:解答题
 x2+8,BC所在抛物线的解析式为y=
x2+8,BC所在抛物线的解析式为y= (x-8)2,且已知B(m,4).
(x-8)2,且已知B(m,4).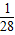 (x-16)2.试求索道的最大悬空高度.
(x-16)2.试求索道的最大悬空高度.
查看答案和解析>>
科目:初中数学 来源:第2章《二次函数》中考题集(27):2.8 二次函数的应用(解析版) 题型:解答题
 x2+8,BC所在抛物线的解析式为y=
x2+8,BC所在抛物线的解析式为y= (x-8)2,且已知B(m,4).
(x-8)2,且已知B(m,4). (x-16)2.试求索道的最大悬空高度.
(x-16)2.试求索道的最大悬空高度.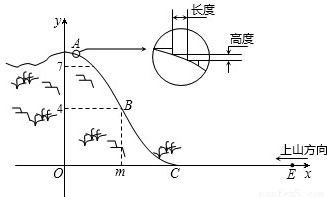
查看答案和解析>>
科目:初中数学 来源:第2章《二次函数》中考题集(24):2.4 二次函数的应用(解析版) 题型:解答题
 x2+8,BC所在抛物线的解析式为y=
x2+8,BC所在抛物线的解析式为y= (x-8)2,且已知B(m,4).
(x-8)2,且已知B(m,4).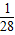 (x-16)2.试求索道的最大悬空高度.
(x-16)2.试求索道的最大悬空高度.
查看答案和解析>>
科目:初中数学 来源:2012年江苏省无锡市蠡园中学中考适应性练习数学试卷(十六)(解析版) 题型:解答题
 x2+8,BC所在抛物线的解析式为y=
x2+8,BC所在抛物线的解析式为y= (x-8)2,且已知B(m,4).
(x-8)2,且已知B(m,4).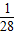 (x-16)2.试求索道的最大悬空高度.
(x-16)2.试求索道的最大悬空高度.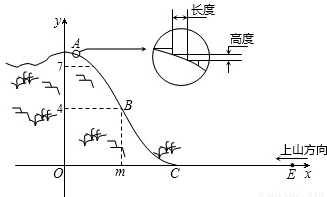
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com