
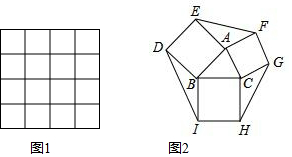
分析 (1)利用勾股定理,结合网格结构画出边长为$\sqrt{17}$,$\sqrt{13}$,$\sqrt{10}$的三角形即可;
(2)利用割补法求面积即可;
(3)根据△ABC的面积,利用割补法即可求出六边形DHIGFE的面积.
解答 解:(1)如图所示,△ABC即为所求.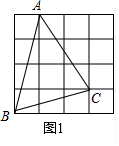
(2)S△ABC=3×4-4×1÷2-3×1÷2-3×2÷2=12-2-1.5-3=5.5;
(3)如图2①中,延长FA到点H,使得AH=AF,连接EH.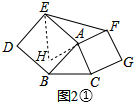
∵四边形ABDE,四边形ACGF是正方形,
∴AB=AE,AF=AC,∠BAE=∠CAF=90°,
∴∠EAF+∠BAC=180°,
∴△AEF和△ABC是两个互补三角形.
∵∠EAH+∠HAB=∠BAC+∠HAB=90°,
∴∠EAH=∠BAC,
∵AF=AC,
∴AH=AB,
在△AEH和△ABC中,
$\left\{\begin{array}{l}{AE=AB}\\{∠EAB=∠BAC}\\{AH=AC}\end{array}\right.$,
∴△AEH≌△ABC,
∴S△AEF=S△AEH=S△ABC,
∴S六边形=17+13+10+4×5.5=62.
点评 本题考查作图-应用与设计,三角形的面积等知识,解题的关键是理解题意,搞清楚互补三角形的面积相等,学会利用割补法求面积,属于中考常考题型.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:选择题
| A. | y1>y2>y3 | B. | y1<y2<y3 | C. | y1>y3>y2 | D. | 不确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-3)2=4 | B. | (x-3)2=14 | C. | (x+3)2=4 | D. | (x+3)2=14 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
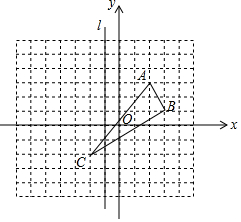 如图,已知△ABC的三个顶点分别为A(2,3),B(3,1),C(-2,-2),直线l是经过(-1,0)且垂直于x轴的一条直线.
如图,已知△ABC的三个顶点分别为A(2,3),B(3,1),C(-2,-2),直线l是经过(-1,0)且垂直于x轴的一条直线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com