
【题目】在平面直角坐标系![]() 中,如果等边三角形的一边与
中,如果等边三角形的一边与![]() 轴平行或在
轴平行或在![]() 轴上,则称这个等边三角形为水平正三角形.
轴上,则称这个等边三角形为水平正三角形.
(1)已知![]() ,
,![]() ,若
,若![]() 是水平正三角形,则点
是水平正三角形,则点![]() 坐标的是_____(只填序号);①
坐标的是_____(只填序号);①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]()
(2)已知点![]() ,
,![]() ,
,![]() ,以这三个点中的两个点及平面内的另一个点
,以这三个点中的两个点及平面内的另一个点![]() 为顶点,构成一个水平正三角形,则这两个点是 ,并求出此时点
为顶点,构成一个水平正三角形,则这两个点是 ,并求出此时点![]() 的坐标;
的坐标;
(3)已知![]() 的半径为
的半径为![]() ,点
,点![]() 是
是![]() 上一点,点
上一点,点![]() 是直线
是直线![]() 上一点,若某个水平正三角形的两个顶点为
上一点,若某个水平正三角形的两个顶点为![]() ,
,![]() ,直接写出点
,直接写出点![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
【答案】(1)点![]() 坐标的是②,④;(2)
坐标的是②,④;(2)![]() 或
或![]() ;(3)点
;(3)点![]() 的横坐标
的横坐标![]() 的取值范围为
的取值范围为![]()
![]() 或
或![]() 或
或![]() .
.
【解析】
(1)利用勾股定理求出![]() 的长,即可知道
的长,即可知道![]() 的坐标;
的坐标;
(2)因为是一个水平正三角形,则这两个点是![]() ,
,![]() ,连接
,连接![]() ,所以
,所以![]() 与
与![]() 轴正方向夹角为
轴正方向夹角为![]() ,然后分①当点
,然后分①当点![]() 在线段
在线段![]() 的左侧时和②当点
的左侧时和②当点![]() 在线段
在线段![]() 的右侧时两种情况讨论;
的右侧时两种情况讨论;
(3)分三种情况:①当![]() 与
与![]() 轴平行或重合时;②当
轴平行或重合时;②当![]() 与
与![]() 轴的负半轴夹角为
轴的负半轴夹角为![]() 时;③当
时;③当![]() 与
与![]() 轴的正半轴夹角为
轴的正半轴夹角为![]() 时;根据水平正三角形的性质求出点
时;根据水平正三角形的性质求出点![]() 的横坐标
的横坐标![]() 的取值范围即可.
的取值范围即可.
(1)∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
当点![]() 在
在![]() 轴上方时,
轴上方时,![]() ,
,
当点![]() 在
在![]() 轴下方时,
轴下方时,![]() ,
,
则点![]() 坐标的是②,④;
坐标的是②,④;
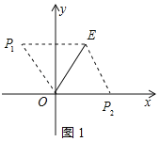
(2)因为是一个水平正三角形,则这两个点是![]() ,
,![]() ,连接
,连接![]() ,如图1所示:
,如图1所示:
∴![]() 与
与![]() 轴正方向夹角为
轴正方向夹角为![]() .
.
①当点![]() 在线段
在线段![]() 的左侧时,
的左侧时,
点![]() 与点
与点![]() 关于
关于![]() 轴对称,
轴对称,
∴![]() ,
,
②当点![]() 在线段
在线段![]() 的右侧时,
的右侧时,
点![]() 在
在![]() 轴上且
轴上且![]() ,
,
∴![]() .
.
∴![]() 或
或![]() ;
;
(3)分三种情况:
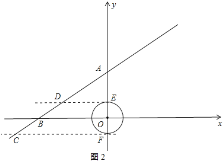
①当![]() 与
与![]() 轴平行或重合时,如图2所示:
轴平行或重合时,如图2所示:
![]() 为
为![]() 的直径,直线
的直径,直线![]() 与坐标轴的交点分别为
与坐标轴的交点分别为![]() 、
、![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
作![]() 轴交直线
轴交直线![]() 于
于![]() ,作
,作![]() 轴交直线
轴交直线![]() 于
于![]() ,
,
则![]() 在线段
在线段![]() 上,
上,![]() ,
,
∴![]() ,
,
同理:![]() ,
,
∴![]() ;
;
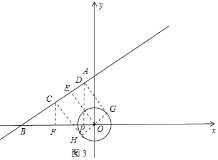
②当![]() 与
与![]() 轴的负半轴夹角为
轴的负半轴夹角为![]() 时,如图3所示:
时,如图3所示:
作![]() 直线
直线![]() 于
于![]() ,作直径
,作直径![]() ,作
,作![]() 、
、![]() ,分别交
,分别交![]() 于
于![]() 、
、![]() ,
,
作![]() 于
于![]() ,作
,作![]() 于
于![]() ,
,
则![]() 在线段
在线段![]() 上,
上,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
同理:![]() ,
,
∴![]() ;
;
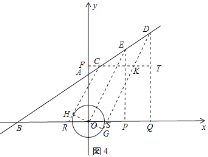
③当![]() 与
与![]() 轴的正半轴夹角为
轴的正半轴夹角为![]() 时,如图4所示:
时,如图4所示:
同②得:![]() .
.
综上所述,点![]() 的横坐标
的横坐标![]() 的取值范围为
的取值范围为![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
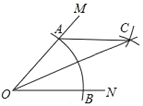
【题目】如图,在∠MON中,以点O为圆心,任意长为半径作弧,交射线OM于点A,交射线ON于点B,再分别以A、B为圆心,OA的长为半径作弧,两弧在∠MON的内部交于点C,作射线OC,若OA=5,AB=6,则点B到AC的距离为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在绿化某县城与高速公路的连接路段中,需购买罗汉松、雪松两种树苗共400株,罗汉松树苗每株60元,雪松树苗每株70元.相关资料表明:罗汉松、雪松树苗的成活率分别为70%,90%.
(1)若购买这两种树苗共用去26500元,则罗汉松、雪松树苗各购买多少株?
(2)绿化工程来年一般都要将死树补上新苗,现要使该两种树苗来年共补苗不多于80株,则罗汉松树苗至多购买多少株?
(3)在(2)的条件下,应如何选购树苗,才能使购买树苗的费用最低?请求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
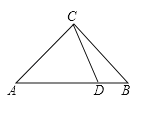
【题目】已知:在Rt△ABC中,∠ACB=90°,AC=BC,D是线段AB上一点,连结CD,将线段CD绕点C逆时针旋转90°得到线段CE,连结DE,BE.
(1)依题意补全图形;
(2)若∠ACD=α,用含α的代数式表示∠DEB;
(3)若△ACD的外心在三角形的内部,请直接写出α的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前“校园手机”现象越来越受到社会关注,针对这种现象,某校九年级数学兴趣小组的同学随机调查了若干名家长对“中学生带手机的”的态度(态度分为:A.无所谓;B.基本赞成;C.赞成;D.反对).并将调查结果绘制成频数折线统计图1和扇形统计图2(不完整).请根据图中提供的信息,解答下列问题:
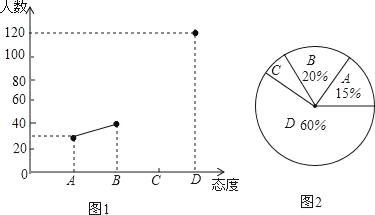
(1)此次抽样调查中,共调查了多少名中学生家长;
(2)求出图2中扇形C所对的圆心角的度数,并将图1补充完整;
(3)在此次调查活动中,初三(1)班有A1、A2两位家长对中学生带手机持反对态度,初三(2)班有B1、B2两位学生家长对中学生带手机也持反对态度,现从这4位家长中选2位家长参加学校组织的家校活动,用列表法或画树状图的方法求出选出的2人来自不同班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,对角线AC,BD交于点O,且AC⊥BC,点E是BC延长线上一点, ![]() ,连接DE.
,连接DE.
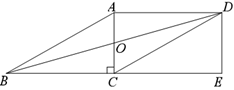
(1)求证:四边形ACED为矩形;
(2)连接OE,如果BD=10,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尺规作图要求:Ⅰ、过直线外一点作这条直线的垂线;Ⅱ、作线段的垂直平分线;
Ⅲ、过直线上一点作这条直线的垂线;Ⅳ、作角的平分线.
如图是按上述要求排乱顺序的尺规作图:

则正确的配对是( )
A. ①﹣Ⅳ,②﹣Ⅱ,③﹣Ⅰ,④﹣Ⅲ B. ①﹣Ⅳ,②﹣Ⅲ,③﹣Ⅱ,④﹣Ⅰ
C. ①﹣Ⅱ,②﹣Ⅳ,③﹣Ⅲ,④﹣Ⅰ D. ①﹣Ⅳ,②﹣Ⅰ,③﹣Ⅱ,④﹣Ⅲ
查看答案和解析>>
科目:初中数学 来源: 题型:
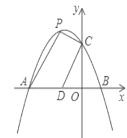
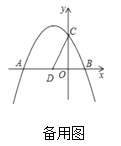
【题目】如图,抛物线![]() 交
交![]() 轴于点
轴于点![]() 和点
和点![]() ,交
,交![]() 轴于点
轴于点![]() .已知点
.已知点![]() 的坐标为
的坐标为![]() ,点
,点![]() 为第二象限内抛物线上的一个动点,连接
为第二象限内抛物线上的一个动点,连接![]() 、
、![]() 、
、![]() .
.
(1)求这个抛物线的表达式.
(2)当四边形![]() 面积等于4时,求点
面积等于4时,求点![]() 的坐标.
的坐标.
(3)①点![]() 在平面内,当
在平面内,当![]() 是以
是以![]() 为斜边的等腰直角三角形时,直接写出满足条件的所有点
为斜边的等腰直角三角形时,直接写出满足条件的所有点![]() 的坐标;
的坐标;
②在①的条件下,点![]() 在抛物线对称轴上,当
在抛物线对称轴上,当![]() 时,直接写出满足条件的所有点
时,直接写出满足条件的所有点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com