
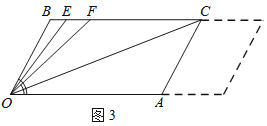
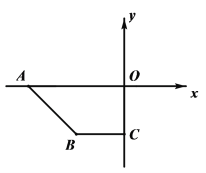
【题目】已知:BC∥OA,∠B=∠A=120°,试回答下列问题:
(1)如图1所示,求证:OB∥AC;

(2)如图2,若点E、F在BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF,则∠EOC的度数是______;

(3)在(2)的条件下,若平行移动AC,其它条件不变,如图3,则∠OCB:∠OFB的值是______.
【答案】(1)证明见解析;(2)30°;(3)1:2
【解析】
(1)依据BC∥OA,即可得到∠A+∠C=180°,根据∠B=∠A,即可得到∠B+∠C=180°,进而得出OB∥AC;
(2)依据BC∥OA,∠B=∠A=120°,即可得到∠AOB=60°,再根据∠FOC=∠AOC,且OE平分∠BOF,即可得出∠EOC=![]() ∠AOB=30°;
∠AOB=30°;
(3)依据BC∥OA,可得∠OCB=∠AOC,∠OFB=∠AOF,再根据∠FOC=∠AOC,即可得到∠AOC:∠AOF=1:2,即∠OCB:∠OFB=1:2.
解:(1)∵BC∥OA,
∴∠A+∠C=180°,
又∵∠B=∠A,
∴∠B+∠C=180°,
∴OB∥AC;
(2)∵BC∥OA,∠B=∠A=120°,
∴∠AOB=60°,
∵∠FOC=∠AOC,且OE平分∠BOF,
∴∠EOF=![]() BOF,∠COF=
BOF,∠COF=![]() ∠AOF,
∠AOF,
∴∠EOC=![]() ∠AOB=30°,
∠AOB=30°,
故答案为:30°;
(3)∵BC∥OA,
∴∠OCB=∠AOC,∠OFB=∠AOF,
∵∠FOC=∠AOC,
∴∠AOC:∠AOF=1:2,
∴∠OCB:∠OFB=1:2.
故答案为:1:2.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知y=ax2+bx+c的图象如图所示,其对称轴为直线x=-1,与x轴的一个交点为(1,0),与y轴的交点在(0,2)与(0,3)之间(不包含端点),有如下结论:①.2a+b=0 ②. 3a+2c<0 ③.a+5b+2c>0;④.-1<a<-![]() ,则结论正确的有_____________.
,则结论正确的有_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,弦CD⊥AB于E,∠CDB=15°,OE=2![]() .
.
(1)求⊙O的半径;
(2)将△OBD绕O点旋转,使弦BD的一个端点与弦AC的一个端点重合,则弦BD与弦AC的夹角为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知∠A=∠F,∠C=∠D,试说明:BD∥CE.
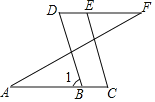
解:∵∠A=∠F(已知)
∴AC∥DF(______)
∴∠D=∠1(______)
又∵∠C=∠D(已知)
∴∠1=______
∴BD∥CE(______)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() ,
,![]() 的方程组
的方程组![]() ,则下列结论中:①当
,则下列结论中:①当![]() 时,方程组的解是
时,方程组的解是![]() ;②当
;②当![]() ,
,![]() 的值互为相反数时,
的值互为相反数时,![]() ;③不存在一个实数
;③不存在一个实数![]() 使得
使得![]() ;④若
;④若![]() ,则
,则![]() 正确的个数有( )
正确的个数有( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在大课间活动中,同学们积极参加体育锻炼,小龙在全校随机抽取一部分同学就“我最喜爱的体育项目”进行了一次抽样调查,下面是他通过收集的数据绘制的两幅不完整的统计图,请你根据图中提供的信息,解答以下问题:
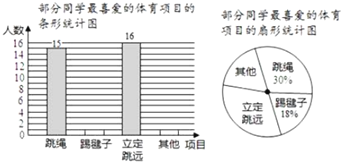
(1)小龙共抽取______名学生;
(2)补全条形统计图;
(3)在扇形统计图中,“其他”部分对应的圆心角的度数是_______;
(4)若全校共2100名学生,请你估算“立定跳远”部分的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(图①为实景侧视图,图②为安装示意图),在屋顶的斜坡面上安装太阳能热水器:先安装支架AB和CD(均与水平面垂直),再将集热板安装在AD上.为使集热板吸热率更高,公司规定:AD与水平线夹角为θ1,且在水平线上的射影AF为1.4 m.现已测量出屋顶斜面与水平面夹角为θ2,并已知tan θ1=1.082,tan θ2=0.412.如果安装工人已确定支架AB高为25 cm,求支架CD的高.(结果精确到1 cm)

查看答案和解析>>
科目:初中数学 来源: 题型:
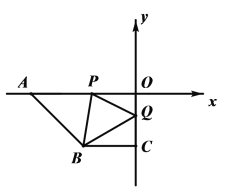
【题目】如图,在平面直角坐标系xOy中,点A(a,0),B(c,c),C(0,c),且满足![]() ,P点从A点出发沿x轴正方向以每秒2个单位长度的速度匀速移动,Q点从O点出发沿y轴负方向以每秒1个单位长度的速度匀速移动.
,P点从A点出发沿x轴正方向以每秒2个单位长度的速度匀速移动,Q点从O点出发沿y轴负方向以每秒1个单位长度的速度匀速移动.
(1)直接写出点B的坐标,AO和BC位置关系是;
(2)当P、Q分别是线段AO,OC上时,连接PB,QB,使![]() ,求出点P的坐标;
,求出点P的坐标;
(3)在P、Q的运动过程中,当∠CBQ=30°时,请探究∠OPQ和∠PQB的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com