

分析 (1)根据题意得出$\left\{\begin{array}{l}{2m+n-13=0}\\{m-n+1=0}\end{array}\right.$,解方程组即可求得A的坐标;
(2)作AM⊥x轴于M,CN⊥AM于N,证得△AMB≌△CAN,从而求得AM=CN=5,AN=BM=2,MN=AM-AN=5-2=3,即可求得C的坐标;
(3)作AM⊥x轴于M,DG⊥AM于G,同理证得D(9,1),证得CD∥x轴,由A(4,5),E(3,0),根据待定系数法求得直线AE和直线CD的解析式,根据斜率即可判定两直线垂直,根据勾股定理求得CD和AE的长即可判断它们的数量关系.
解答 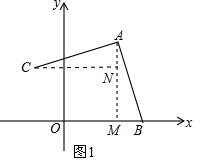 解:(1)∵$\sqrt{2m+n-13}$+|m-n+1|=0,
解:(1)∵$\sqrt{2m+n-13}$+|m-n+1|=0,
∴$\left\{\begin{array}{l}{2m+n-13=0}\\{m-n+1=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=4}\\{n=5}\end{array}\right.$,
∴点A的坐标(4,5);
(2)如图1,作AM⊥x轴于M,CN⊥AM于N,
∵点A的坐标(4,5),B(6,0),
∴AM=5,BM=6-4=2,
∵∠BAC=90°,
∴∠MAB+∠CAN=90°,
∵∠MAB+∠ABM=90°,
∴∠ABM=∠CAN,
在△AMB和△CAN中,
$\left\{\begin{array}{l}{∠ABM=∠CAN}\\{∠AMB=∠CNA=90°}\\{AB=AC}\end{array}\right.$,
∴△AMB≌△CAN(AAS),
∴AM=CN=5,AN=BM=2,
∴MN=AM-AN=5-2=3,
∴C(-1,3);
(3)如图2,作AM⊥x轴于M,DG⊥AM于G,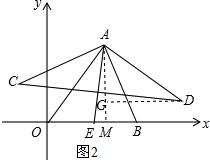
同理证得D(9,1),
∵C(-1,3),
∴直线CD的解析式为y=-$\frac{1}{5}$x+$\frac{14}{5}$,CD=$\sqrt{(9+1)^{2}+(3-1)^{2}}$=2$\sqrt{26}$,
∵A(4,5),E(3,0),
∴直线AE的解析式为y=5x-15,AE=$\sqrt{(4-3)^{2}+{5}^{2}}$=$\sqrt{26}$,
∵-$\frac{1}{5}$×5=-1,
∴AE⊥CD,CD=2AE,
∴AE垂直平分CD,且CD=2AE.
点评 本题考查了全等三角形的判定和性质,等腰三角形的判定和性质,待定系数法求直线的解析式,勾股定理的应用,作出辅助线构建全等三角形是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
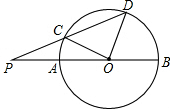 如图,已知直径BA与弦DC的延长线交于点P,且PC=CO,$\widehat{CD}$=$\widehat{AC}$+$\widehat{DB}$,求∠DOB的度数.
如图,已知直径BA与弦DC的延长线交于点P,且PC=CO,$\widehat{CD}$=$\widehat{AC}$+$\widehat{DB}$,求∠DOB的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
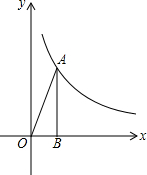 如图,点A(2,m)在双曲线y=$\frac{k}{x}$上,AB⊥x轴,B为垂足,tan∠AOB=2.
如图,点A(2,m)在双曲线y=$\frac{k}{x}$上,AB⊥x轴,B为垂足,tan∠AOB=2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,拦水坝的横断面为梯形ABCD,坝高23米.坝面宽BC=6米.根据条件求:
如图,拦水坝的横断面为梯形ABCD,坝高23米.坝面宽BC=6米.根据条件求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com