
【题目】某学校举行演讲比赛,选出了10名同学担任评委,并事先拟定从如下4个方案中选择合理的方案来确定每个演讲者的最后得分(满分为10分):
方案①:所有评委所给分的平均数;
方案②:在所有评委所给分中,去掉一个最高分和一个最低分,然后再计算其余给分的平均数;
方案③:所有评委所给分的中位数;
方案④:所有评委所给分的众数。
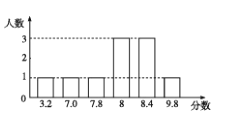
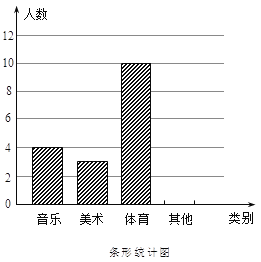
为了探究上述方案的合理性,先地某个同学的演讲成绩进行了统计实验,如图是这个同学的得分统计图。
(1)分别按上述4个方案计算这个同学演讲的最后得分;
(2)根据(1)中的结果,请用统计的知识说明哪些方案不适合作为这个同学演讲的最后得分,并说明你的理由。
【答案】(1)见解析;(2)见解析.
【解析】
本题关键是理解每种方案的计算方法:
(1)方案1:平均数=总分数÷10.
方案2:平均数=去掉一个最高分和一个最低分的总分数÷8.
方案3:10个数据,中位数应是第5个和第6个数据的平均数.
方案4:求出评委给分中,出现次数最多的分数.
(2)考虑不受极值的影响,不能有两个得分等原因进行排除.
(1)方案1最后得分:![]() ×(3.2+7.0+7.8+3×8+3×8.4+9.8)=7.7;
×(3.2+7.0+7.8+3×8+3×8.4+9.8)=7.7;
方案2最后得分:![]() ×(7.0+7.8+3×8+3×8.4)=8;
×(7.0+7.8+3×8+3×8.4)=8;
方案3最后得分:8;
方案4最后得分:8或8.4.
(2)因为方案1中的平均数受极端数值的影响,不适合作为这个同学演讲的最后得分,
所以方案1不适合作为最后得分的方案.
因为方案4中的众数有两个,众数失去了实际意义,所以方案4不适合作为最后得分的方案.


科目:初中数学 来源: 题型:
【题目】(2017浙江省湖州市,第23题,10分)湖州素有鱼米之乡之称,某水产养殖大户为了更好地发挥技术优势,一次性收购了20000kg淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养10天的总成本为30.4万元;放养20天的总成本为30.8万元(总成本=放养总费用+收购成本).
(1)设每天的放养费用是a万元,收购成本为b万元,求a和b的值;
(2)设这批淡水鱼放养t天后的质量为m(kg),销售单价为y元/kg.根据以往经验可知:m与t的函数关系为![]() ;y与t的函数关系如图所示.
;y与t的函数关系如图所示.
①分别求出当0≤t≤50和50<t≤100时,y与t的函数关系式;
②设将这批淡水鱼放养t天后一次性出售所得利润为W元,求当t为何值时,W最大?并求出最大值.(利润=销售总额﹣总成本)

查看答案和解析>>
科目:初中数学 来源: 题型:
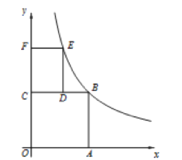
【题目】如图,正方形OABC的边OA,OC在坐标轴上,矩形CDEF的边CD在CB上,且5CD=3CB,边CF在轴上,且CF=2OC-3,反比例函数y=![]() (k>0)的图象经过点B,E,则点E的坐标是____
(k>0)的图象经过点B,E,则点E的坐标是____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AM是中线,AD是高线.
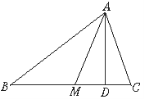
(1)若AB比AC长4 cm,则△ABM的周长比△ACM的周长多__________ cm.
(2)若△AMC的面积为12 cm2,则△ABC的面积为__________cm 2.
(3)若AD又是△AMC的角平分线,∠AMB=130°,求∠ACB的度数.(写过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
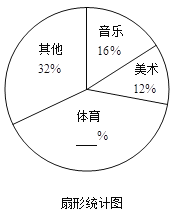
【题目】为了解学生的课余生活情况,某中学在全校范围内随机抽取部分学生进行问卷调查. 问卷中请学生选择最喜欢的课余生活种类(每人只选一类),选项有音乐类、美术类、体育类及其他共四类,调查后将数据绘制成扇形统计图和条形统计图(如图所示).
(1)体育所占的百分比是_______,选择其他的人数是________
(2)在问卷调查中,小丁和小李分别选择了音乐类和美术类,校学生会要从选择音乐类和美术类的学生中分别抽取一名学生参加活动,用列表或画树状图的方法求小丁和小李恰好都被选中的概率;
(3)如果该学校有500名学生,请你估计该学校中最喜欢体育运动的学生约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】跳绳时,绳甩到最高处时的形状是抛物线.正在甩绳的甲、乙两名同学拿绳的手间距AB为6米,到地面的距离AO和BD均为0.9米,身高为1.4米的小丽站在距点O的水平距离为1米的点F处,绳子甩到最高处时刚好通过她的头顶点E.以点O为原点建立如图所示的平面直角坐标系, 设此抛物线的解析式为y=ax2+bx+0.9.
(1)求该抛物线的解析式;
(2)如果小华站在OD之间,且离点O的距离为3米,当绳子甩到最高处时刚好通过他的头顶,请你算出小华的身高;
(3)如果身高为1.4米的小丽站在OD之间,且离点O的距离为t米, 绳子甩到最高处时超过她的头顶,请结合图像,写出t的取值范围 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,函数![]() 的图象与函数
的图象与函数![]() 的图象交于点
的图象交于点![]() ,
,![]() .
.
(1)求函数![]() 的表达式;
的表达式;
(2)观察图象,直接写出不等式![]() 的解集;
的解集;
(3)若点![]() 是
是![]() 轴上的动点,当
轴上的动点,当![]() 周长最小时,求点
周长最小时,求点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点 E,F 是ABCD 对角线上两点,在条件①DE=BF;②∠ADE=∠CBF; ③AF=CE;④∠AEB=∠CFD 中,添加一个条件,使四边形 DEBF 是平行四边形,可添加 的条件是( )
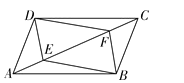
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以四边形ABCD的边AB、AD为底边分别作等腰三角形ABF和ADE,连接EB.
(1)当四边形ABCD为正方形时(如图1),以边AB、AD为斜边分别向外侧作等腰直角三角形ABF和ADE,连接EB、FD,线段EB和FD的数量关系是 .
(2)当四边形ABCD为矩形时(如图2),以边AB、AD为斜边分别向内侧作等腰直角三角形ABF和ADE,连接EF、BD,线段EF和BD具有怎样的数量关系?请加以证明;
(3)当四边形ABCD为平行四边形时(如图3),以边AB、AD为斜边分别向平行四边形内测、外侧作等腰直角三角形ABF和ADE,且△EAD与△FBA的顶角都为α,连接EF、BD,交点为G,请用α表示出∠EGD,并说明理由.
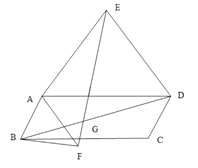
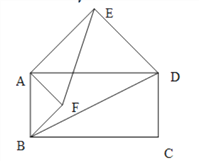
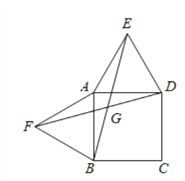
图1 图2 图3
【答案】(1)EF=BD;(2)EF=![]() BD;(3)
BD;(3)![]()
【解析】分析:(1)正方形的性质、等边三角形的性质和全等三角形的证明方法可证明△AFD≌△ABE,由全等三角形的性质即可得到EB=FD;(2)根据等腰直角三角形的性质可得![]() ,再证得∠BAD=∠FAE,即可判定△BAD∽△FAE ,根据相似三角形的性质可得
,再证得∠BAD=∠FAE,即可判定△BAD∽△FAE ,根据相似三角形的性质可得![]() ,即可得
,即可得![]() ;(3)
;(3)![]() ,先证△BFA∽△DEA,即可得
,先证△BFA∽△DEA,即可得![]() ,
,
再证得![]() ,所以△BAD∽△FAE,根据全等三角形的性质即可得
,所以△BAD∽△FAE,根据全等三角形的性质即可得![]() ,再由∠AHE=∠DHG,即可得
,再由∠AHE=∠DHG,即可得![]() .
.
详解:(1)EF=BD,
理由如下:
四边形ABCD为正方形,
∴AB=AD,
∵以四边形ABCD的边AB、AD为边分别向外侧作等边三角形ABF和ADE,
∴AF=AE,∠FAB=∠EAD=60°,
∵∠FAD=∠BAD+∠FAB=90°+60°=150°,
∠BAE=∠BAD+∠EAD=90°+60°=150°,
∴∠FAD=∠BAE,
在△AFD和△ABE中, 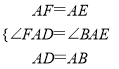 ,
,
∴△AFD≌△ABE,
∴EB=FD;
(2)EF=![]() BD.
BD.
证明:∵△AFB为等腰直角三角形
∴![]() ,∠FAB=45°
,∠FAB=45°
同理: ![]() ,∠EAD=45° ∴∠BAD+∠FAD=∠EAD+∠DAF
,∠EAD=45° ∴∠BAD+∠FAD=∠EAD+∠DAF
即∠BAD=∠FAE
∵![]() ,
, ![]() ∴
∴![]()
∴△BAD∽△FAE ∴![]()
即: ![]()
(3)解: ![]()
∵△AFB为等腰直角三角形,∴FB=FA,
同理:ED=EA,∴![]() ,
,
又∵![]() ,∴△BFA∽△DEA,
,∴△BFA∽△DEA,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴△BAD∽△FAE,
∴![]() ,
,
又∵∠AHE=∠DHG,
∴![]() .
.
点睛:本题考查了正方形的性质、全等三角形的判定和性质、等边三角形的性质等腰直角三角形的先证、相似三角形的判定和性质,题目的综合性很强,难度也不小,解题的关键是对特殊几何图形的性质要准确掌握.
【题型】解答题
【结束】
27
【题目】如图,二次函数![]() 的图象交x轴于A、B两点,交y轴于点C,点B的坐标为(3,0),顶点C的坐标为(1,4).连接BC.
的图象交x轴于A、B两点,交y轴于点C,点B的坐标为(3,0),顶点C的坐标为(1,4).连接BC.
(1)求二次函数的解析式和直线BC的解析式;
(2)点M是直线BC上的一个动点(不与B、C重合),过点M作x轴的垂线,交抛物线于点N,交x轴于点P.
①如图1,求线段MN长度的最大值;
②如图2,连接AM,QN,QP.试问:抛物线上是否存在点Q,使得![]() 与
与![]() 的面积相等,且线段NQ的长度最小?如果存在,求出点Q的坐标;如果不存在,请说明理由.
的面积相等,且线段NQ的长度最小?如果存在,求出点Q的坐标;如果不存在,请说明理由.

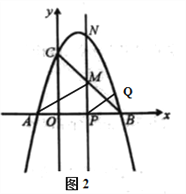
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com