
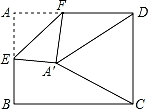
【题目】如图,在矩形纸片ABCD中,AB=4,BC=4![]() ,点E是AB的中点,点F是AD边上的一个动点,将△AEF沿EF所在直线翻折,得到△A'EF,连接A'C,A'D,则当△A'DC是以A'D为腰的等腰三角形时,FD的长是_____.
,点E是AB的中点,点F是AD边上的一个动点,将△AEF沿EF所在直线翻折,得到△A'EF,连接A'C,A'D,则当△A'DC是以A'D为腰的等腰三角形时,FD的长是_____.
【答案】4![]() ﹣2或3
﹣2或3![]()
【解析】
存在两种情况:当A′D=DC,连接ED,勾股定理求得ED的长,可判断E,A′,D三点共线,根据勾股定理即可得到结论;当A′D=A′C,证明AEA′F是正方形,于是得到结论.
解:①当A′D=DC时,如图1,连接ED,
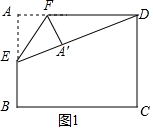
∵点E是AB的中点,AB=4,BC=4![]() ,四边形ABCD是矩形,
,四边形ABCD是矩形,
∴AD=BC=4![]() ,∠A=90°,
,∠A=90°,
∴DE=![]() =6,
=6,
∵将△AEF沿EF所在直线翻折,得到△A'EF,
∴A′E=AE=2,
∵A′D=DC=AB=4,
∴DE=A′E+A′D=6,
∴点E,A′,D三点共线,
∵∠A=90°,
∴∠FA′E=∠FA′D=90°,
设AF=x,则A′F=x,FD=4![]() -x,
-x,
在Rt△FA′D中,42+x2=(4![]() -x)2,
-x)2,
解得:x=![]() ,
,
∴FD=3![]() ;
;
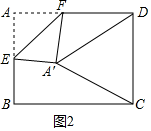
②当A′D=A′C时,如图2,
∵A′D=A′C,
∴点A′在线段CD的垂直平分线上,
∴点A′在线段AB的垂直平分线上,
∵点E是AB的中点,
∴EA′是AB的垂直平分线,
∴∠AEA′=90°,
∵将△AEF沿EF所在直线翻折,得到△A'EF,
∴∠A=∠EA′F=90°,AF=FA′,
∴四边形AEA′F是正方形,
∴AF=AE=2,
∴DF=4![]() -2,
-2,
故答案为:4![]() -2或3
-2或3![]() .
.


科目:初中数学 来源: 题型:
【题目】红树林学校在七年级新生中举行了全员参加的“防溺水”安全知识竞赛,试卷题目共10题,每题10分.现分别从三个班中各随机取10名同学的成绩(单位:分),收集数据如下:
1班:90,70,80,80,80,80,80,90,80,100;
2班:70,80,80,80,60,90,90,90,100,90;
3班:90,60,70,80,80,80,80,90,100,100.
整理数据:
分数 人数 班级 | 60 | 70 | 80 | 90 | 100 |
1班 | 0 | 1 | 6 | 2 | 1 |
2班 | 1 | 1 | 3 |
| 1 |
3班 | 1 | 1 | 4 | 2 | 2 |
分析数据:
平均数 | 中位数 | 众数 | |
1班 | 83 | 80 | 80 |
2班 | 83 |
|
|
3班 |
| 80 | 80 |
根据以上信息回答下列问题:
(1)请直接写出表格中![]() 的值;
的值;
(2)比较这三组样本数据的平均数、中位数和众数,你认为哪个班的成绩比较好?请说明理由;
(3)为了让学生重视安全知识的学习,学校将给竞赛成绩满分的同学颁发奖状,该校七年级新生共570人,试估计需要准备多少张奖状?
查看答案和解析>>
科目:初中数学 来源: 题型:
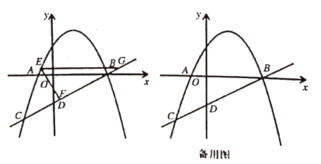
【题目】如图,二次函数![]() 的图象经过点
的图象经过点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() 为二次函数图象上任一点.
为二次函数图象上任一点.
![]() 求这个二次函数的解析式;
求这个二次函数的解析式;
![]() 若点
若点![]() 在直线
在直线![]() 的上方,过
的上方,过![]() 分别作
分别作![]() 和
和![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于不同的两点
于不同的两点![]() (
(![]() 在
在![]() 的左侧),求
的左侧),求![]() 周长的最大值;
周长的最大值;
![]() 是否存在点
是否存在点![]() 使得
使得![]() 是以
是以![]() 为直角边的直角三角形?如果存在,直接写出点
为直角边的直角三角形?如果存在,直接写出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2-2ax+c与x轴分别交于点A、B(点B在点A的右侧),与y轴交于点C,连接BC,点(![]() ,
,![]() a-3)在抛物线上.
a-3)在抛物线上.
(1)求c的值;
(2)已知点D与C关于原点O对称,作射线BD交抛物线于点E,若BD=DE,①求抛物线所对应的函数表达式 ;②过点B作BF⊥BC交抛物线的对称轴于点F,以点C为圆心,以![]() 的长为半径作⊙C,点T为⊙C上的一个动点,求
的长为半径作⊙C,点T为⊙C上的一个动点,求![]() TB+TF的最小值.
TB+TF的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某海域有A、B、C三艘船正在捕鱼作业,C船突然出现故障,向A、B两船发出紧急求救信号,此时B船位于A船的北偏西72°方向,距A船24海里的海域,C船位于A船的北偏东33°方向,同时又位于B船的北偏东78°方向.
(1)求∠ABC的度数;
(2)A船以每小时30海里的速度前去救援,问多长时间能到出事地点.(结果精确到0.01小时).
(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]()
![]() 的图象相交于
的图象相交于![]() ,
,![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,连接
,连接![]() ,且
,且![]() 的面积为2.
的面积为2.
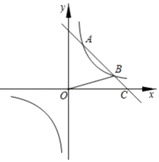
(1)求反比例函数的表达式;
(2)将直线![]() 向下平移,若平移后的直线与反比例函数的图象只有一个交点,试说明直线
向下平移,若平移后的直线与反比例函数的图象只有一个交点,试说明直线![]() 向下平移了几个单位长度?
向下平移了几个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司组织员工到附近的景点旅游,根据旅行社提供的收费方案,绘制了如图所示的图象,图中折线ABCD表示人均收费y(元)与参加旅游的人数x(人)之间的函数关系.
(1)当参加旅游的人数不超过10人时,人均收费为 元;
(2)如果该公司支付给旅行社3600元,那么参加这次旅游的人数是多少?
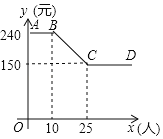
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市计划印制一批宣传册该宣传册每本共![]() 页,由
页,由![]() 两种彩页构成,已知
两种彩页构成,已知![]() 种彩页制版费
种彩页制版费![]() 元/张,
元/张,![]() 种彩页制版费
种彩页制版费![]() 元/张,该宣传册的制版费共计
元/张,该宣传册的制版费共计![]() 元(注:彩页制版费与印数无关)
元(注:彩页制版费与印数无关)
![]() 每本宣传册
每本宣传册![]() 两种彩页各有多少张;
两种彩页各有多少张;
![]() 据了解,
据了解,![]() 种彩页印刷费
种彩页印刷费![]() 元/张,
元/张,![]() 种彩页印刷费
种彩页印刷费![]() 元/张,这批宣传册的制版费与印刷费的和不超过
元/张,这批宣传册的制版费与印刷费的和不超过![]() 元如果按到该市展台处的参观者人手一册发放宣传册,预计最多能发给多少位参观者.
元如果按到该市展台处的参观者人手一册发放宣传册,预计最多能发给多少位参观者.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对于平面直角坐标系![]() 中的线段
中的线段![]() 和点
和点![]() ,在
,在![]() 中,当
中,当![]() 边上的高为2时,称
边上的高为2时,称![]() 为
为![]() 的“等高点”,称此时
的“等高点”,称此时![]() 为
为![]() 的“等高距离”.
的“等高距离”.
(1)若点![]() 的坐标为(1,2),点
的坐标为(1,2),点![]() 的坐标为(4,2),则在点
的坐标为(4,2),则在点![]() (1,0),
(1,0),![]() (
(![]() ,4),
,4),![]() (0,3)中,
(0,3)中,![]() 的“等高点”是点___;
的“等高点”是点___;
(2)若![]() (0,0),
(0,0),![]() =2,当
=2,当![]() 的“等高点”在
的“等高点”在![]() 轴正半轴上且“等高距离”最小时,点
轴正半轴上且“等高距离”最小时,点![]() 的坐标是__.
的坐标是__.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com