
【题目】如图,抛物线y=﹣![]() x2+bx+c,经过矩形OABC的A(3,0),C(0,2),连结OB.D为横轴上一个动点,连结CD,以CD为直径作⊙M,与线段OB有一个异于点O的公共点E,连结DE.过D作DF⊥DE,交⊙M于F.
x2+bx+c,经过矩形OABC的A(3,0),C(0,2),连结OB.D为横轴上一个动点,连结CD,以CD为直径作⊙M,与线段OB有一个异于点O的公共点E,连结DE.过D作DF⊥DE,交⊙M于F.
(1)求抛物线的解析式;
(2)tan∠FDC的值;
(3)①当点D在移动过程中恰使F点落在抛物线上,求此时点D的坐标;
②连结BF,求点D在线段OA上移动时,BF扫过的面积.

【答案】(1) y=﹣![]() x2+
x2+![]() x+2;(2)
x+2;(2)![]() ;(3)①(﹣
;(3)①(﹣![]() ,0);②3
,0);②3
【解析】
(1)将点A、C的坐标代入抛物线的表达式,即可求解;
(2) 连接CE、CF、FO,证明∠FDC=∠ECD=∠EOD=∠BOA,即可求解;
(3) ①如图2,连接FO,则∠FOG=∠FCD,证明∠FOG=∠FCD=∠CDE=∠COE,通过tan∠FOG=tan∠COB=![]() ,来确定直线OF的表达式,进而求解;
,来确定直线OF的表达式,进而求解;
②如图3,当点D、O重合时,连接CF、BF,由①知tan∠FOG=![]() ,设FG=3a,则OG=2a=HC,HF=2﹣GF=2﹣3a,由①同理可得:△CHF∽△FGO,则
,设FG=3a,则OG=2a=HC,HF=2﹣GF=2﹣3a,由①同理可得:△CHF∽△FGO,则![]() ,求得a的值,根据BF扫过的面积为△BOF的面积,即可求解.
,求得a的值,根据BF扫过的面积为△BOF的面积,即可求解.
解:(1)将点A、C的坐标代入抛物线的表达式得: ,
,
解得: ,
,
故抛物线的解析式为:y=﹣![]() x2+
x2+![]() x+2;
x+2;
(2)如图1,连接CE、CF、FO,
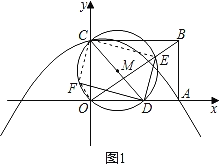
∵CD是直径,
∴∠CED=90°,即CE⊥DE,
又∵DF⊥DE,
∴∠FDC=∠ECD=∠EOD=∠BOA,
∴tan∠FDC=tan∠BOA=![]() ;
;
(3)①如图2,
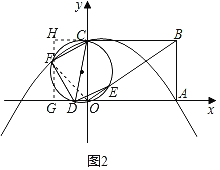
连接FO,则∠FOG=∠FCD,
∵CD是直径,
∴∠CFD=90°,
同理∠FDE=90°,
∴FC∥DE,
∴∠FCD=∠CDE=∠COE,
∴∠FOG=∠FCD=∠CDE=∠COE,
∴tan∠FOG=tan∠COE=tan∠COB=![]() ,
,
故直线OF的表达式为:y=﹣![]() x②,
x②,
联立①②并解得: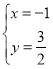 ,故点F(﹣1,
,故点F(﹣1,![]() );
);
过点F作y轴的平行线GH,交x轴于点G,交过点C与x轴的平行线于点H,
∴FG=![]() ,CH=1,HF=2﹣
,CH=1,HF=2﹣![]() =
=![]() ,
,
∵∠HFC+∠GFD=90°,∠HFC+∠HCF=90°,
∴∠HCF=∠GFD,
又∠CHF=∠FGD=90°,
∴△CHF∽△FGD,
∴![]() ,即
,即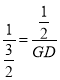 ,解得:GD=
,解得:GD=![]() ,
,
∴OD=1﹣![]() =
=![]() ,
,
故点D的坐标为:(﹣![]() ,0);
,0);
②如图3,当点D、O重合时,连接CF、BF,

则BF扫过的面积为△BOF的面积,∠CFO=90°,
过点F作y轴的平行线HG,交x轴于点G,交过点C与x轴的平行线于点H,
由①同理可得:△CHF∽△FGO,则![]() ,
,
由①知tan∠FOG=![]() ,设FG=3a,则OG=2a=HC,HF=2﹣GF=2﹣3a,
,设FG=3a,则OG=2a=HC,HF=2﹣GF=2﹣3a,
∴![]() ,解得:a=
,解得:a=![]() ;
;
在Rt△FOG中,FO=![]() ,
,
同理在Rt△AOB中,OB=![]() ,
,
∵EF是圆的直径,故OF⊥OE,
BF扫过的面积=S△BOF=![]() ×BO×FO=
×BO×FO=![]() ,
,
故BF扫过的面积为3.


科目:初中数学 来源: 题型:
【题目】为了预防新冠肺炎,某药店销售甲、乙两种防护口罩,已知甲口罩每袋的售价比乙口罩多5元,小明从该药店购买了3袋甲口罩和2袋乙口罩共花费115元.
(1)求该药店甲、乙两种口罩每袋的售价分别为多少元?
(2)根据消费者需求,药店决定用不超过8000元购进甲、乙两种口罩共400袋.已知甲口罩每袋的进价为22.2元,乙口罩每袋的进价为17.8元,要使药店获利最大,应该购进甲、乙两种口罩各多少袋,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
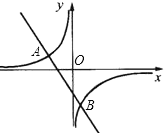
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A(﹣2,1),B(1,n)两点.
的图象交于A(﹣2,1),B(1,n)两点.
(1)求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值>反比例函数的值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司计划投资![]() 万元引进一条汽车配件流水生产线,经过调研知道该流水生产线的年产量为
万元引进一条汽车配件流水生产线,经过调研知道该流水生产线的年产量为![]() 件,每件总成本为
件,每件总成本为![]() 万元,每件出厂价
万元,每件出厂价![]() 万元;流水生产线投产后,从第
万元;流水生产线投产后,从第![]() 年到第
年到第![]() 年的维修、保养费用累计
年的维修、保养费用累计![]() (万元)如下表:
(万元)如下表:
第 |
|
|
|
|
|
| ··· |
维修、保养费用累计 |
|
|
|
|
|
| ··· |
若上表中第![]() 年的维修、保养费用累计
年的维修、保养费用累计![]() (万元)与
(万元)与![]() 的数量关系符合我们已经学过的一次函数、二次函数、反比例函数中某一个.
的数量关系符合我们已经学过的一次函数、二次函数、反比例函数中某一个.
(1)求出![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)投产第几年该公司可收回![]() 万元的投资?
万元的投资?
(3)投产多少年后,该流水线要报废(规定当年的盈利不大于维修、保养费用累计即报费)?
查看答案和解析>>
科目:初中数学 来源: 题型:
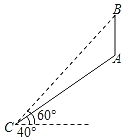
【题目】如图,在一坡角40°,坡面长AC=100m的小山顶上安装了一电信基站AB,在山底的C处,测得塔顶仰角为60°,求塔的高AB.(精确到0.1m)(以下供参考:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(2,m),B(-2,3m)分别在反比例函数![]() 和
和![]() 的图象上,经过点A、B的直线与y轴相交于点C.
的图象上,经过点A、B的直线与y轴相交于点C.
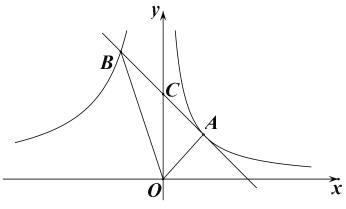
(1)求m和k的值;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知汽车燃油箱中的y(单位:升)与该汽车行驶里程数x(单位:千米)是一次函数关系.贾老师从某汽车租赁公司租借了一款小汽车,拟去距离出发地600公里的目的地旅游(出发之前,贾老师往该汽车燃油箱内注满了油).行驶了200千米之后,汽车燃油箱中的剩余油量为40升;又行驶了100千米,汽车燃油箱中的剩余油量为30升.
(1)求y关于x的函数关系式(不要求写函数的定义域);
(2)当汽车燃油箱中的剩余油量为8升的时候,汽车仪表盘上的燃油指示灯就会亮起来.在燃油指示灯亮起来之前,贾老师驾驶该车可否抵达目的地?请通过计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
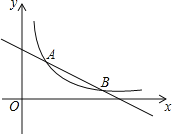
【题目】如图,已知反比例函数y=![]() (x>0)的图象与一次函数y=﹣
(x>0)的图象与一次函数y=﹣![]() x+4的图象交于A和B(6,n)两点.
x+4的图象交于A和B(6,n)两点.
(1)求k和n的值;
(2)若点C(x,y)也在反比例函数y=![]() (x>0)的图象上,求当2≤x≤6时,函数值y的取值范围.
(x>0)的图象上,求当2≤x≤6时,函数值y的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com