
����Ŀ����1����ͼ�١�1����2���B����C��ʲô��ϵ��Ϊʲô��
��2����ͼ�١�ABC��DE�۵����õ�ͼ�ڣ���գ���1����2_______��B����C(����������������=��)������A��40��ʱ����B����C����1����2��______.
��3����ͼ��,����ͼ�ٵ���ABC��DE�۵��õ���,�����A��30��,��x��y��360�㣭����B����C����1����2����360�㣭 �� ,�����BDA����CEA���A�Ĺ�ϵΪ

���𰸡�������.
��������
���⣨1�������������ڽ���180�ȿɵó�����1+��2=��B+��C����2����ABC��DE�۵�����1+��2=��B+��C���Ӷ��������A=40��ʱ����B+��C+��1+��2=140��2=280������3���������ϼ���ɹ��ɳ�һ����ɣ���BDA+��CEA=2��A��
���������
�⣺��1����1+��2 = ��B+��C���������£�
����ADE����1+��2 = 180��- ��A
����ABC����B+��C = 180��- ��A
�� ��1+��2 = ��B+��C
��2���ߡ�1+��2+��BDE+��CED=��B+��C+��BDE+��CED=360�������1+��2=��B+��C������A=40��ʱ����B+��C+��1+��2=140��2=280��
��3�������A=30������x+y=360��-����B+��C+��1+��2��=360��-300��=60����������BDA+��CEA����A�Ĺ�ϵΪ����BDA+��CEA=2��A.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ṩ���¶�������ֱ���������У�30���������Ե�ֱ�DZ���б�ߵ�һ�룬
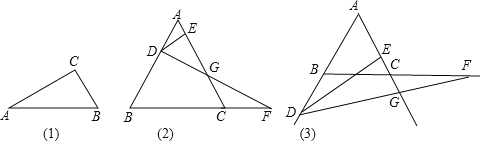
��ͼ(1)��Rt��ABC�У���C=90�㣬��A=30�㣬��BC=![]() AB��
AB��
���������϶������й�֪ʶ������������⣺
��ͼ(2)���߳�Ϊ6�ĵȱ�������ABC�У���D��A������������AB������A��B�˶���Fͬʱ��C����������ͬ���ٶ���������BC�����˶�������D��DE��AC��DF������AC�ڵ�G��
(1)����D�˶���AB���е�ʱ��ֱ��д��AE�ij���
(2)��DF��ABʱ����AD�ij�����BDF�������
(3)С��ͨ���������֣�����D���߶�AB��ʱ��EG�ij�ʼ�յ���AC��һ�룬���뵱��D�˶���ͼ3�����ʱ��EG�ij�ʼ�յ���AC��һ����?���ı䣬˵�����ɣ������䣬˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��� A �� y ���������ϵ� B �� x �Ḻ�����ϣ��� AB=2����BAO=15������ P ���߶�OA �ϵ�һ�����㣬�� PB ![]() PA ����СֵΪ_____________��
PA ����СֵΪ_____________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
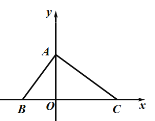
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ABO�����Ϊ8��OA��OB��BC��12����P�������ǣ�a��6����
(1) ��ABC�������������ֱ�ΪA�� �� ����B�� �� ����C�� �� ����
(2) �Ƿ���ڵ�P��ʹ��![]() �������ڣ�����������������е�P�����꣮
�������ڣ�����������������е�P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ı��ε�һ��������Ի�һ���Խ��ߣ��Ұ��ı��ηֳ����������Σ�������ε�һ��������Ի������Խ��ߣ��Ұ�����ηֳ����������Σ�......���룺��n���ε�һ��������Ի�_________���Խ��ߣ��Ұ�n���ηֳ� _________�������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ��һ�꼶��350��ͬѧȥ���Σ���֪2��A�ͳ���1��B�ͳ�������ѧ��100�ˣ�1��A�ͳ���2��B�ͳ�������ѧ��110��.
(1)A��B�ͳ�ÿ���ɷֱ���ѧ�������ˣ�
(2)���ƻ�����A�ͳ�![]() ��������B�ͳ�
��������B�ͳ�![]() ��������������������һ����������ѧ������ǡ��ÿ����������.
��������������������һ����������ѧ������ǡ��ÿ����������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��l��y=mx��m+1��mΪ��������m��0���������ύ��A��B���㣬����AOB��O��ԭ�㣩�����ǡΪ2�������Ҫ���ֱ��l�У� ��
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
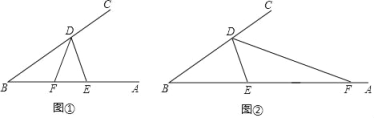
����Ŀ����֪��D��E�ֱ��ǡ�B������BC��BA�ϵĵ㣬��DEB��2��B��FΪBA��һ�㣮
��1����ͼ�٣���DFƽ�֡�BDE����֤��BD��DE+EF��
��2����ͼ�ڣ���DFΪ��DBE�����ƽ���ߣ�BD��DE��EF������������������ϵ����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У������ɸ�������(�ᡢ�������Ϊ����)����˳��ͼ�з������У���(1��0)��(2��0)��(2��1)��(3��1)��(3��0)���� �����������̽���ɵã���50���������Ϊ�� ��
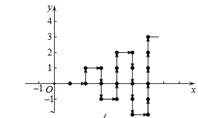
A. (10����5)B. (10����1) C. (10��0) D. (10��1��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com