
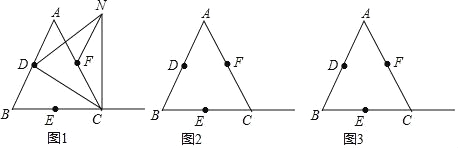
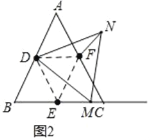
����Ŀ����֪��ABC�ǵȱ������Σ���D��E��F�ֱ��DZ�AB��BC��AC���е㣬��M������EC�ϵ�һ�����㣬���ȱߡ�DMN��ʹ��DMN���ABC��BC��ͬ�࣬����NF��
��1����ͼ1������M���C�غ�ʱ��ֱ��д���߶�FN���߶�EM��������ϵ��
��2������M���߶�EC�ϣ���M���E��C���غϣ�ʱ����ͼ2�������ⲹȫͼ�Σ����жϣ�1���еĽ����Ƿ����������������֤����������������˵�����ɣ�
��3������DF��ֱ��DM��ֱ��AC�ཻ�ڵ�G������DNF������ǡ�GMC�����9����AB=8����ֱ��д���߶�CM�ij���
���𰸡���1��FN=EM����2��ͼ�μ�������FN=EM������֤������������3��1��2��
��������
(1)������ED��EF��DF������D��E��F�ֱ��DZ�AB��BC��AC���е㣬�ó���DEF�ǵȱ������Σ������ж���DFN�ա�DEM��SAS�������ɵó�FN=EM����2���루1�����ƣ�������ED��EF��DF���ó���DEF�ǵȱ������Σ������ж���DFN�ա�DEM��SAS�������ɵó�FN=EM����3��������������ٵ�M���߶�CE��ʱ������DE��EF������DEF�ǵȱ������Σ��ٸ��������ж���GCM�ס�DEM���������������ε����ʣ��ó�![]() ���ٸ���CE=
���ٸ���CE=![]() BC=4�����ɵó�CM=
BC=4�����ɵó�CM=![]() CE=1���ڵ�M���߶�EC�ӳ�����ʱ������ͬ���ķ������ж���GCM�ס�DEM���ó�
CE=1���ڵ�M���߶�EC�ӳ�����ʱ������ͬ���ķ������ж���GCM�ס�DEM���ó�![]() ����
����![]() ���ٸ���CE=4�����ɵó�CM=
���ٸ���CE=4�����ɵó�CM=![]() CE=2��
CE=2��
��1���߶�FN���߶�EM��������ϵΪ��FN=EM��
���ɣ���ͼ1������ED��EF��DF��
�ߡ�ABC�ǵȱ������Σ�
��AB=BC=AC��
��D��E��F�ֱ��DZ�AB��BC��AC���е㣬
��DE=EF=FD������DEF�ǵȱ������Σ�
���FDE=60�㣬
�֡ߡ�DMN�ǵȱ������Σ�
��DN=DM����MDN=60�㣬
���FDN=��EDM��
�ڡ�FDN�͡�EDM�У�
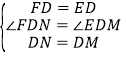 ��
��
���DFN�ա�DEM��SAS����
��FN=EM��
��2����ȫͼ�Σ���ͼ2������FN=EM������
֤��������ED��EF��DF��
�ߡ�ABC�ǵȱ������Σ�
��AB=BC=AC��
��D��E��F�ֱ��DZ�AB��BC��AC���е㣬
��DE=EF=FD������DEF�ǵȱ������Σ�
���FDE=60�㣬
�֡ߡ�DMN�ǵȱ������Σ�
��DN=DM����MDN=60�㣬
���FDN=��EDM��
�ڡ�FDN�͡�EDM�У�
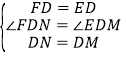 ��
��
���DFN�ա�DEM��SAS����
��FN=EM��
��3�������������
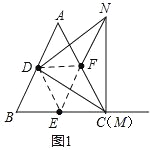
����ͼ3����M���߶�CE��ʱ������DE��EF�����DEF�ǵȱ������Σ�
�ɣ�2���ɵá�DFN�ա�DEM��
���DFN���DEM�����ȣ�
�ߡ�DNF������ǡ�GMC�����9����
���DEM������ǡ�GMC�����9����
��CG��DE��
���GCM�ס�DEM��
��![]() ��
��
�֡�CE=![]() BC=
BC=![]() ��8=4��
��8=4��
��CM=![]() CE=1��
CE=1��
����ͼ4����M���߶�EC�ӳ�����ʱ������DE��EF�����DEF�ǵȱ������Σ�
ͬ���ɵá�DFN�ա�DEM��
���DFN���DEM�����ȣ�
�ߡ�DNF������ǡ�GMC�����9����
���DEM������ǡ�GMC�����9����
��CG��DE��
���GCM�ס�DEM��
��![]() ����
����![]() ��
��
�֡�CE=![]() BC=4��
BC=4��
��CM=![]() CE=2��
CE=2��
����������CM�ij�Ϊ1��2��


 �ִʾ��ƪϵ�д�
�ִʾ��ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ɽֲ��������A��B����������֪A��Ϊ�����Σ���Ϊ��x+y���ף���Ϊ��x��y���ף�B��Ϊ�����Σ��߳�Ϊ��x+3y���ף�
��1�����ô���ʽ��ʾA��B���������֮�Ͳ�����
��2���ָ���ʵ����Ҫ��A���������ģ������ӣ�11x��y���ף������٣�x��2y���ף����ĺ�A���ij��ȿ���350�ף������ĺ��������ܳ�֮��Ϊ980�ף�
����x��y��ֵ��
����A��ȫ����ֲC�ֻ���B��ȫ����ֲD�ֻ�����C��D���ֻ�Ͷ��ķ����������ο͵����������

�����ĺ�A��B�������εľ�����֮�ͣ���������=���橁Ͷ�룩
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ������ȤС���ڱ�Уѧ���п�չ���ж��й�2016�������Ƚ��¼�֪�����ר���������ȡ��������ķ�ʽ�����ʾ����飬�ʾ�����Ľ����ΪA��B��C��D���࣬���У�A���ʾ���dz��˽⡱��B���ʾ���Ƚ��˽⡱��C���ʾ�������˽⡱��D���ʾ����̫�˽⡱����������������������±���
��� | A | B | C | D |
Ƶ�� | 30 | 40 | 24 | b |
Ƶ�� | a | 0.4 | 0.24 | 0.06 |

��1�����е�a= �� b=��
��2�����ݱ������ݣ�������ͳ��ͼ�����ΪB��ѧ��������Ӧ������Բ�ĽǵĶ�����
��3������У��ѧ��1000�������ݵ��������Ƹ�Уѧ�������ΪD������ԼΪ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCΪ����ֱ�������Σ���D�DZ�BC��һ���㣬��ADΪֱ�DZ�������ֱ�ǡ�ADE���ֱ��A��E����BC�������ߣ�����ֱ�ΪF��G������BE��
��1��֤����BG=FD��
��2�����ABE�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2+5x+3��3m=0����������ȵ�ʵ������
��1����m��ȡֵ��Χ��
��2����mΪ�����������ʱ���̵ĸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ȤС�������λ��һ�������˵�A��B֮��ľ��룬�鳤С������С���Ա������ֱ��ABƽ�еĵ�·EF���ߣ������ߵ���C������á�ACF=45�㣬����ǰ����100�����D������á�BDF=60�㣬��֪AB��EF֮��ľ���Ϊ60�ף���A��B����ľ��룮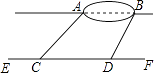
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
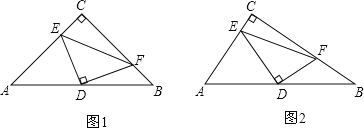
����Ŀ����֪����ͼ1��Rt��ABC�У���ACB=90�㣬DΪAB�е㣬DE��DF�ֱ�AC��E����BC��F����DE��DF��
��1�����CA=CB����֤��AE2+BF2=EF2��
��2����ͼ2�����CA��CB����1���н��ۻ��ܳ���������������֤����������������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ACB��90�㣬BC��6���ֱ��Ե�A�͵�CΪԲ�ģ�����ͬ�ij������� ![]() AC��Ϊ�뾶�����������ཻ�ڵ�M�͵�N �� ��ֱ��MN��AB�ڵ�D �� ��AC�ڵ�E �� ����CD �� ��DE�ij�Ϊ ��
AC��Ϊ�뾶�����������ཻ�ڵ�M�͵�N �� ��ֱ��MN��AB�ڵ�D �� ��AC�ڵ�E �� ����CD �� ��DE�ij�Ϊ �� 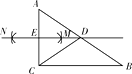
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����AOB��ֱ�ǣ���AOC=40����ON����AOC��ƽ���ߣ�OM����BOC��ƽ���ߣ�

��1������MON�Ĵ�С.
��2���������AOC�Ĵ�С�����ı�ʱ����MON�Ĵ�С�Ƿ����ı䣿Ϊʲô��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com