
分析 由于关于x的方程k2x2-2(k+1)x+1=0有实数根,
①当k=0时,方程为一元一次方程,此时一定有实数根;
②当k≠0时,方程为一元二次方程,如果方程有实数根,那么其判别式是一个非负数,由此即可求出k的取值范围.
解答 解:当k=0时,原方程可化为-2x+1=0,此方程有实数根;
当k≠0时,由题意得:[-2(k+1)]2-4k2≥0,
解得:k≥-$\frac{1}{2}$,
综上,k的取值范围是k≥-$\frac{1}{2}$,
故答案为:k≥-$\frac{1}{2}$.
点评 本题考查了一元二次方程根的判别式的应用.此题要注意题干并没有说明方程一定是一元二次方程,因此要将所有的情况都考虑到.


科目:初中数学 来源: 题型:解答题
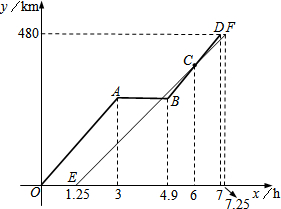 “十•一”长假,小王与小叶相约分别驾车从南京出发,沿同一路线驶往距南京480km的甲地旅游.小王由于有事临时耽搁,比小叶迟出发1.25小时.而小叶的汽车中途发生故障,等排除故障后,立即加速赶往甲地.若从小叶出发开始计时,图中的折线O-A-B-D、线段EF分别表示小叶、小王两人与南京的距离y1(km)、y2(km)与时间x(h)之间的函数关系.
“十•一”长假,小王与小叶相约分别驾车从南京出发,沿同一路线驶往距南京480km的甲地旅游.小王由于有事临时耽搁,比小叶迟出发1.25小时.而小叶的汽车中途发生故障,等排除故障后,立即加速赶往甲地.若从小叶出发开始计时,图中的折线O-A-B-D、线段EF分别表示小叶、小王两人与南京的距离y1(km)、y2(km)与时间x(h)之间的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
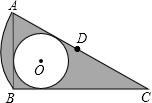 如图,在Rt△ABC中,AB=1,∠ACB=30°,点D是AC的中点,⊙O是△ABC的内切圆,以点D为圆心,以AD的长为半径作$\widehat{AB}$,则图中阴影部分的面积是$\frac{3\sqrt{3}-5}{6}$π+$\frac{\sqrt{3}}{4}$.
如图,在Rt△ABC中,AB=1,∠ACB=30°,点D是AC的中点,⊙O是△ABC的内切圆,以点D为圆心,以AD的长为半径作$\widehat{AB}$,则图中阴影部分的面积是$\frac{3\sqrt{3}-5}{6}$π+$\frac{\sqrt{3}}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 分数 | 80 | 85 | 90 | 85 |
| 人数 | 2 | 3 | 4 | 1 |
| A. | 95和85 | B. | 90和85 | C. | 90和87.5 | D. | 85和87.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6 | B. | $\frac{1}{2}$ | C. | 2 | D. | $\frac{11}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com