
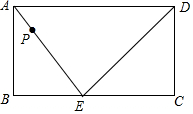
 ��ͼ���ھ���ABCD�У���E��BC���ϣ�����P��2����/����ٶȴӵ�A�������ء�AED�ı߰���A��E��D��A��˳���˶�һ�ܣ����P��A������x��x��0�����ABP�������y��
��ͼ���ھ���ABCD�У���E��BC���ϣ�����P��2����/����ٶȴӵ�A�������ء�AED�ı߰���A��E��D��A��˳���˶�һ�ܣ����P��A������x��x��0�����ABP�������y������ ��1�����ABE�У���AE�ϵĸ�Ϊh����S��ABE=$\frac{1}{2}$AE•h=$\frac{1}{2}$AB•BE��AP=2x�����ɽ�����⣮
��2���ֱ��������P���߶�AE��ʱ������P���߶�AD��ʱ��x��ȡֵ��Χ���ɽ�����⣮
��� �⣺��1�����ı���ABCD�Ǿ��Σ�
���ABE=90�㣮
�� AB=8��BE=6��
��AE=$\sqrt{82+62}$=10��
���ABE�У���AE�ϵĸ�Ϊh��
��S��ABE=$\frac{1}{2}$AE•h=$\frac{1}{2}$AB•BE��
��h=$\frac{24}{5}$���� AP=2x��
��y=$\frac{24}{5}$x��0��x��5����
��2�� ���ı���ABCD�Ǿ��Σ�
���ı���ABCD�Ǿ��Σ�
���B=��C=90�㣬AB=DC��AD=BC��
��EΪBC�е㣬
��BE=EC��
���ABE�ա�DCE��
��AE=DE��
����P�˶�����Dʱ��S��ABP=S��ABD��������� $\frac{12}{5}$x=32-4x��
���x=5��
����P�˶�һ�ܻص���Aʱ��S��ABP=0���������32-4x=0��
���x=8��
��AD=2����8-5��=6��
��BC=6��
��BE=3��
��AE+ED=2��5=10��
��AE=5��
��Rt��ABE��AB=$\sqrt{52-32}$=4��
���ABE�У���AE�ϵĸ�Ϊh��
��S��ABE=$\frac{1}{2}$AE•h=$\frac{1}{2}$AB•BE��
��h=$\frac{12}{5}$��
�� AP=2x��
�൱��P��A�˶�����Dʱ��y=$\frac{12}{5}$x��0��x��2.5����
��y����x�ĺ�������ʽΪ����0��x��5ʱ��y=$\frac{12}{5}$x����5��x��8ʱ��y=32-4x��
���� ���⿼�麯����Ӧ�ã����ε����ʡ������ε������֪ʶ������Ĺؼ����������⣬���������ѧ֪ʶ������⣬�����п��������ͣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -3x2+6xy-3y2 | B�� | 3x2-6xy-y2 | C�� | 3x2-6xy+3y2 | D�� | -3x2-6xy-3y2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ƽ��ֱ������ϵ�У���A��0��4$\sqrt{3}$����B��m��-2$\sqrt{3}$����C��n��-2$\sqrt{3}$������m��n����$\sqrt{m+3n}$+��n-6��2=0���߶�BC��y���ڵ�H��
��ƽ��ֱ������ϵ�У���A��0��4$\sqrt{3}$����B��m��-2$\sqrt{3}$����C��n��-2$\sqrt{3}$������m��n����$\sqrt{m+3n}$+��n-6��2=0���߶�BC��y���ڵ�H���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���ڡ�ABC�У���C=90�㣬��BAC=30�㣬AB=8��ADƽ�֡�BAC����PQ�ֱ���AB��AD���ϵĶ��㣬��PQ+BQ����Сֵ�ǣ�������
��ͼ���ڡ�ABC�У���C=90�㣬��BAC=30�㣬AB=8��ADƽ�֡�BAC����PQ�ֱ���AB��AD���ϵĶ��㣬��PQ+BQ����Сֵ�ǣ�������| A�� | 4 | B�� | 5 | C�� | 6 | D�� | 7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
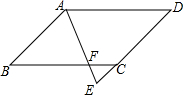 ��ͼ���ı���ABCD��ƽ���ı��Σ�AEƽ�֡�BAD����DC���ӳ����ڵ�E��AB=3��EF=0.8��AF=2.4����AD�ij���
��ͼ���ı���ABCD��ƽ���ı��Σ�AEƽ�֡�BAD����DC���ӳ����ڵ�E��AB=3��EF=0.8��AF=2.4����AD�ij����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
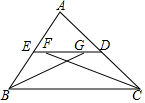 ��ͼ���ڡ�ABC�У�ED��BC����ABC�͡�ACB��ƽ���߷ֱ�ED�ڵ�G��F����FG=2��ED=6����EB+DC=8��
��ͼ���ڡ�ABC�У�ED��BC����ABC�͡�ACB��ƽ���߷ֱ�ED�ڵ�G��F����FG=2��ED=6����EB+DC=8���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com