
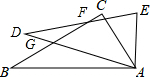
 如图,△ABC≌△ADE,∠DAC=60°,∠BAE=100°,BC分别交AD、DE于点G、F,求∠DFB的度数.
如图,△ABC≌△ADE,∠DAC=60°,∠BAE=100°,BC分别交AD、DE于点G、F,求∠DFB的度数.  轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
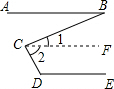 完成下面的证明:
完成下面的证明:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
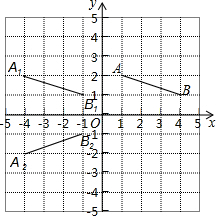 如图,在平面直角坐标系中,线段AB的两个端点的坐标分别为(1,2)、(4,1),
如图,在平面直角坐标系中,线段AB的两个端点的坐标分别为(1,2)、(4,1),查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,-1),P5(2,-1),P6(2,0),…,则点P2017的坐标是(672,1).
如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,-1),P5(2,-1),P6(2,0),…,则点P2017的坐标是(672,1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com