
【题目】经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,这三种可能性大小相同,现在两辆汽车经过这个十字路口.
(1)请用“树形图”或“列表法”列举出这两辆汽车行驶方向所有可能的结果;
(2)求这两辆汽车都向左转的概率.
【答案】
(1)
解:两辆汽车所有9种可能的行驶方向如下:
甲汽车 乙汽车 | 左转 | 右转 | 直行 |
左转 | (左转,左转) | (右转,左转) | (直行,左转) |
右转 | (左转,右转) | (右转,右转) | (直行,右转) |
直行 | (左转,直行) | (右转,直行) | (直行,直行) |
(2)
解:由上表知:两辆汽车都向左转的概率是: ![]() .
.
【解析】(1)利用树形图”或“列表法”即可求出两辆汽车行驶方向所有可能的结果;(2)根据(1)中的列表情况即可求出这两辆汽车都向左转的概率.
【考点精析】利用列表法与树状图法对题目进行判断即可得到答案,需要熟知当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx+2过B(﹣2,6),C(2,2)两点. 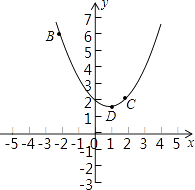
(1)试求抛物线的解析式;
(2)记抛物线顶点为D,求△BCD的面积;
(3)若直线y=﹣ ![]() x向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.
x向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红家有一块L形的菜地,要把L形的菜地按如图所示分成两块面积相等的梯形,种上不同的蔬菜.这两个梯形的上底都是a m,下底都是b m,高都是(b-a) m.
(1)求小红家这块L形菜地的面积.(用含a、b的代数式表示)
(2)若a2+b2=15,ab=5,求小红家这块L形菜地的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=30°,点B1、B2、B3…和A1、A2、A3…分别在OM和ON上,且△A1B1A2、△A2B2A3、△A3B3A4、…分别为等边三角形,已知OA1=1,则△A2018B2018A2019的边长为_____.
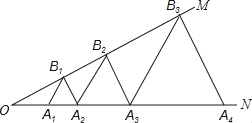
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°.如果将该三角形绕点A按顺时针方向旋转到△AB1C1的位置,点B1恰好落在边BC的中点处.那么旋转的角度等于( )
A.55°
B.60°
C.65°
D.80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为践行党的群众路线,六盘水市教育局开展了大量的教育教学实践活动,如图是其中一次“测量旗杆高度”的活动场景抽象出的平面几何图形.
活动中测得的数据如下:
①小明的身高DC=1.5m
②小明的影长CE=1.7cm
③小明的脚到旗杆底部的距离BC=9cm
④旗杆的影长BF=7.6m
⑤从D点看A点的仰角为30°
请选择你需要的数据,求出旗杆的高度.(计算结果保留到0.1,参考数据 ![]() ≈1.414.
≈1.414. ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:阅读下列材料:已知二次三项式2x2+x+a有一个因式是(x+2),求另一个因式以及a 的值
解:设另一个因式是(2x+b),
根据题意,得2x2+x+a=(x+2)(2x+b),
展开,得2x2+x+a =2x2+(b+4)x+2b,
所以![]() ,解得
,解得![]() ,
,
所以,另一个因式是(2x3),a 的值是6.
请你仿照以上做法解答下题:已知二次三项式3x2 10x m 有一个因式是(x+4),求另一个因式以及m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形OABC在直角坐标系中的位置如图所示,A、C两点的坐标分别为A(10,0)、C(0,3),直线 ![]() 与BC相交于点D,抛物线y=ax2+bx经过A、D两点.
与BC相交于点D,抛物线y=ax2+bx经过A、D两点.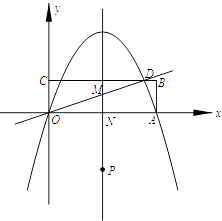
(1)求抛物线的解析式;
(2)连接AD,试判断△OAD的形状,并说明理由.
(3)若点P是抛物线的对称轴上的一个动点,对称轴与OD、x轴分别交于点M、N,问:是否存在点P,使得以点P、O、M为顶点的三角形与△OAD相似?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在同一直角坐标系中,反比例函数y= ![]() 与二次函数y=﹣x2+2x+c的图象交于点A(﹣1,m).
与二次函数y=﹣x2+2x+c的图象交于点A(﹣1,m).
(1)求m、c的值;
(2)求二次函数图象的对称轴和顶点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com