Question

如图，△ABC中，AB=AC，I为△ABC的内心，AI的延长线交△ABC的外接圆于点D，过点I作BC的平行线分别交AB、AC于E、F，若O是△DEF外接圆的圆心．
证明：（1）O点在线段AD上；
（2）AB、AC是⊙O的切线．
如图，四边形ABCD中，∠ADC=60°，∠ABC=30°，DA=DC，求证，BD²=AB²+BC²．

Answer 1

证明：（1）∵AB=AC，I为△ABC的内心，即AI平分∠BAC
∴
又∵BC∥EF，
∴AI垂直平分EF，
而O是△DEF外接圆的圆心，则O点一定在EF的垂直平分线上，
∴O点在线段AD上；

（2）连接OE，OF，BD，BI，如图，
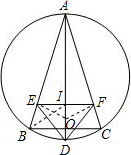
∵AD垂直平分BC，
∴AD过△ABC外接圆的圆心，即AD为△ABC外接圆的直径，
∴∠ABD=90°，而∠AIE=90°，
∴I、E、B、D四点共圆，
∴∠IDE=∠IBE=∠IBC，而∠EOI=2∠EDI，
∴∠EOI=∠ABC，而∠ABC+∠BAD=90°，
∴∠EOI+∠BAD=90°，即∠OEA=90°，
∴AB是⊙O的切线．同理可得AC是⊙O的切线．

证明：
连接AC，因为AD=DC，∠ADC=60°
则△ACD是等边三角形，
过B作BE⊥AB，使BE=BC，连接CE，AE，
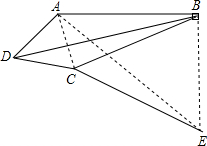
则∠EBC=90°-∠ABC=90°-30°=60°，
∴△BCE是正三角形，
又∠ACE=∠ACB+∠BCE=∠ACB+60°
∠DCB=∠ACB+∠ACD=∠ACB+60°
∴∠ACE=∠DCB
又DC=AC，BC=CE
所以△DCB≌△ACE
所以AE=BD
在直角三角形ABE中AE²=AB²+BE²，
即BD²=AB²+BC²．
分析：（1）由AB=AC，I为△ABC的内心，得AI垂直平分BC，而BC∥EF，得到AI垂直平分EF，所以O点一定在EF的垂直平分线上；
（2）连OE，OF，BD，BI，由AD为△ABC外接圆的直径，易知I、E、B、D四点共圆，所以∠IDE=∠IBE=∠IBC，∠EOI=2∠EDI，∴∠EOI=∠ABC，而∠ABC+∠BAD=90°，得∠EOI+∠BAD=90°，即∠OEA=90°．
连接AC，过B作BE⊥AB，使BE=BC，连接CE，AE，则△ACD，△BCE是等边三角形，易证△DCB≌△ACE，AE=BD，在直角三角形ABE中AE²=AB²+BE²，即BD²=AB²+BC²．
点评：本题考查了圆的切线的判定方法．经过半径的外端点与半径垂直的直线是圆的切线．当已知直线过圆上一点，要证明它是圆的切线，则要连接圆心和这个点，证明这个连线与已知直线垂直即可；当没告诉直线过圆上一点，要证明它是圆的切线，则要过圆心作直线的垂线，证明垂线段等于圆的半径．同时考查了三角形内心的性质和几何中辅助线的作法．