
| A. | $\frac{\sqrt{2015}}{{2}^{2015}}$ | B. | -$\frac{\sqrt{2015}}{{2}^{2015}}$ | C. | $\frac{\sqrt{2016}}{{2}^{2015}}$ | D. | -$\frac{\sqrt{2016}}{{2}^{2015}}$ |
分析 观察所给数字可知:第一个数字是-$\frac{\sqrt{2}}{2}$=-$\frac{\sqrt{2}}{{2}^{1}}$;第二个数字是-$\frac{\sqrt{3}}{4}$=-$\frac{\sqrt{3}}{{2}^{2}}$;第三个数字是$\frac{1}{4}$=$\frac{\sqrt{4}}{{2}^{3}}$;第四个数字是-$\frac{\sqrt{5}}{16}$=-$\frac{\sqrt{5}}{{2}^{4}}$;继而即可总结规律,求出第2015个数.
解答 解:观察可以发现:第一个数字是-$\frac{\sqrt{2}}{2}$=-$\frac{\sqrt{2}}{{2}^{1}}$;
第二个数字是-$\frac{\sqrt{3}}{4}$=-$\frac{\sqrt{3}}{{2}^{2}}$;
第三个数字是$\frac{1}{4}$=$\frac{2}{8}$=$\frac{\sqrt{4}}{{2}^{3}}$;
第四个数字是-$\frac{\sqrt{5}}{16}$=-$\frac{\sqrt{5}}{{2}^{4}}$;
…;
可得第2015个数即是-$\frac{\sqrt{2016}}{{2}^{2015}}$,
故选D.
点评 本题主要考查了数字变化,算式平方根的性质,数列规律问题,找出一般规律是解题的关键.


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:选择题
| A. | 4.15×107 | B. | 4.15×108 | C. | 41.5×107 | D. | 41.5×108 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
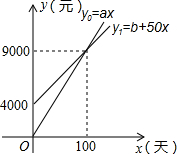 国家推行“节能减排,低碳经济“的政策后,某企业推出一种叫“CNG”的改烧汽油为天然气的装置,每辆车改装费为b元,据市场调查知:每辆车改装前、后的燃料费(含改装费)y0、y1(单位:元)与正常运营时间(单位:天)之间分别满足关系式:y0=ax,y1=b+50x,如图所示,试根据图象解决下列问题:
国家推行“节能减排,低碳经济“的政策后,某企业推出一种叫“CNG”的改烧汽油为天然气的装置,每辆车改装费为b元,据市场调查知:每辆车改装前、后的燃料费(含改装费)y0、y1(单位:元)与正常运营时间(单位:天)之间分别满足关系式:y0=ax,y1=b+50x,如图所示,试根据图象解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 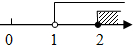 | B. | 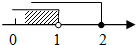 | C. |  | D. | 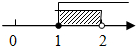 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com