
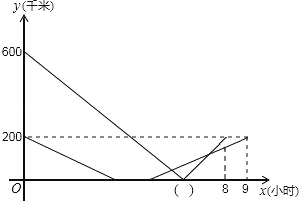
����Ŀ���ס�����������ͨA��B��C���صĹ�·����ʻ���׳���A�س���������C����ʻ��ͬʱ�ҳ���C�س���������b����ʻ������B�ز���B��ͣ��1Сʱ��ԭ·ԭ�ٷ��ص�C�أ���������ʻ�Ĺ����У��ס���������B�ص�·��y��ǧ�ף�����ʻʱ��x��Сʱ��֮��ĺ���ͼ����ͼ��ʾ������ͼ��ش��������⣺
��1����ס����������ٶȣ�����ͼ�У� ����������ȷ������
��2�����ҳ���B�ط��ص�C�صĹ����У�y��x֮��ĺ�����ϵʽ��
��3�����ס���������ʻ����B�ص�·�����ʱ���ס���������B�ص�·���Ƕ��٣�
���𰸡���1��6����2��y=50x-250��5��x��9������3��![]() ��100ǧ�ף�
��100ǧ�ף�
��������
�����������1������֪ͼ������ס��ҵ��ٶȣ�
��2������ͼ���ϵĵ�������ҳ���B�ط��ص�C�صĺ�������ʽ��
��3��������׳���A�ص�B�صĺ�������ʽ��y1=k1x+b1���ͼ׳���B�ص�C�صĺ�������ʽ��y2=k2x+b2������֪�������ʽ��ϣ�2������Ľ���ʽ��⣮
�����������1������֪ͼ��ã����ٶ�Ϊ����600+200����8=100km/h���ҵ��ٶ�Ϊ��200+200���£�9-1��=50km/h��
���ٶ�Ϊ��100km/h����B�����600km��
��ʱ��=![]() =6��
=6��
��2�����ҳ���B�ط��ص�C�صĺ�������ʽ��y=kx+b��
���ҵ��ٶ�Ϊ��200+200���£�9-1��=50km/h��
���ҵ�B�ص�ʱ����200��50=4��Сʱ����
4+1=5��
����M��5��0������ͼ��
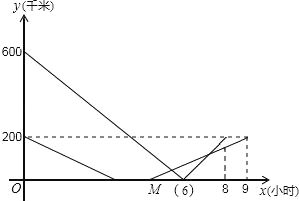
��ͼ��M��5��0������9��200�����㣮
��5k+b=0��9k+b=200
��ã�![]() ��
��
��y=50x-250��
���ҳ���B�ط��ص�C�صĹ����У�y��x֮��ĺ�����ϵʽΪy=50x-250��5��x��9����
��3����׳���A�ص�B�صĺ�������ʽ��y1=k1x+b1��
��ͼ����0��600������6��0�����㣬
��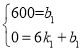 ����ã�
����ã�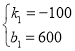 ��
��
��y1=-100x+600��
��׳���B�ص�C�صĺ�������ʽ��y2=k2x+b2��
��ͼ����8��200������6��0�����㣬
��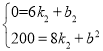 ����ã�
����ã�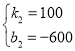 ��
��
��y2=100x-600��
�� ��
��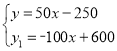 ��
��
��ã�y=![]() ��ǧ�ף���y=100��ǧ�ף���
��ǧ�ף���y=100��ǧ�ף���
�𣺵��ס���������ʻ����B�ص�·�����ʱ���ס���������B�ص�·����![]() ��100ǧ�ף�
��100ǧ�ף�


 �·Ƿ��̸����100��ϵ�д�
�·Ƿ��̸����100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȷ���ǣ�������
A. 4a2����2a��2=2a2 B. ����a+b������a��b��=a2��b2
C. ����a2��a3=a6 D. ����x��2��x=��x
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ����( )
A. ֱ�����ң�����ֱ�� B. ��Բ����Գ�ͼ��
C. ���۹�Բ����һ�㣬ֻ����һ��ֱ�� D. ֱ���ij����ǰ뾶��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=����x+2��2��3����ƽ����3����λ����ôƽ�ƺ������ߵĶ��������ǣ�������
A. ����5����3�� B. ����2��0�� C. ����1����3�� D. ��1����3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУΪ����ǿѧ�����ʣ�����������������������Ŀ��A������ B��ƹ����C����ë�� D������Ϊ�˽�ѧ����ϲ����һ�ֻ��Ŀ�������ȡ�˲���ѧ�����е��飬�������������Ƴ���������������ͳ��ͼ��

��ش��������⣺
��1����α������ѧ�����ж����ˣ�
��2�����㽫����ͳ��ͼ��2������������
��3����ƽʱ��ƹ������Ŀѵ���У��ס��ҡ����������˱������㣬�־�����������ͬѧ����ѡ�����μ�ƹ�����������ǡ��ѡ�мס�����λͬѧ�ĸ��ʣ�����״ͼ���б������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ���ڵ�A����1��2���͵�B����1��6���ĶԳ����ǣ� ��
A.x��
B.y��
C.ֱ��y��4
D.ֱ��x����1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ������˵������2a+b=0�ڵ�-1��x��3ʱ��y��0������x1��y1������x2��y2���ں���ͼ���ϣ���x1��x2ʱ��y1��y2��9a+3b+c=0������ȷ���ǣ� ��
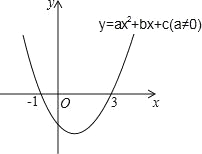
A���٢ڢ� B���٢� C���٢ڢ� D���ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����ȷ���ǣ�������
A. a2+a2��a4B. 3��a��b����3a��b
C. ����b2��3����b5D. a2a2��a4
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com