
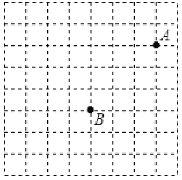
【题目】在正方形网格中建立平面直角坐标系![]() ,使得
,使得![]() ,
,![]() 两点的坐标分别为
两点的坐标分别为![]() ,
,![]() ,过点
,过点![]() 作
作![]() 轴于点C,
轴于点C,
(1)按照要求画出平面直角坐标系![]() ,线段
,线段![]() ,写出点
,写出点![]() 的坐标__________;
的坐标__________;
(2)直接写出以![]() ,
,![]() ,
,![]() 为顶点的三角形的面积___________;
为顶点的三角形的面积___________;
(3)若线段![]() 是由线段
是由线段![]() 平移得到的,点
平移得到的,点![]() 的对应点是
的对应点是![]() ,写出一种由线段
,写出一种由线段![]() 得到线段
得到线段![]() 的过程________.
的过程________.
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c的对称轴是x=﹣1.且过点(0.5,0),有下列结论:
①abc>0; ②a﹣2b+4c=0; ③25a﹣10b+4c=0; ④3b+2c>0;⑤a﹣b≥m(am﹣b).
其中所有正确的结论是( )
A.①②③
B.①③④
C.①②③⑤
D.①③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,E,F分别为BC,CD的中点,AE与BF相交于点G.
(1)如图1,求证:AE⊥BF;
(2)如图2,将△BCF沿BF折叠,得到△BPF,延长FP交BA的延长线于点Q,若AB=4,求QF的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.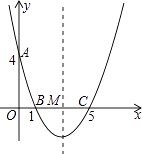
(1)求抛物线的解析式和对称轴;
(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=9,AD=6,∠ADC的平分线交AB于点E,交CB的延长线于点F,AG⊥DE,垂足为G.若AG=4 ![]() ,则△BEF的面积是( )
,则△BEF的面积是( )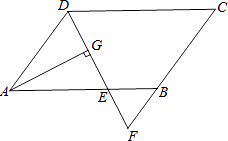
A.![]()
B.2 ![]()
C.3 ![]()
D.4 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
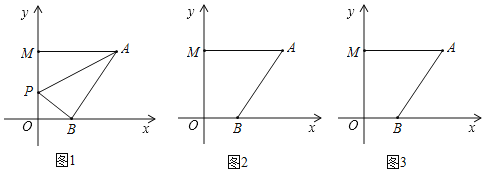
【题目】在平面直角坐标系中,A(6,a),B(b,0),M(0,c),P点为y轴上一动点,且(b﹣2)2+|a﹣6|+![]() =0.
=0.
(1)求点B、M的坐标;
(2)当P点在线段OM上运动时,试问是否存在一个点P使S△PAB=13,若存在,请求出P点的坐标与AB的长度;若不存在,请说明理由.
(3)不论P点运动到直线OM上的任何位置(不包括点O、M),∠PAM、∠APB、∠PBO三者之间是否都存在某种固定的数量关系,如果有,请利用所学知识找出并证明;如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
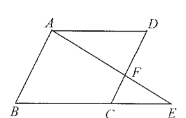
【题目】已知:如图,AD∥BE,∠B=∠D,直线AB与DC平行吗?说明理由(请在下面的解答过程的空格内填空或在括号内填写理由)。
解:直线AB与DC平行.理由如下:
∵ AD∥BE (已知 )
∴ ∠D = ∠DCE ( )
又∵∠B = ∠D ( )
∴∠B = ∠_____ (等量代换)
∴ AB∥DC ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公园有一个抛物线形状的观景拱桥ABC,其横截面如图所示,在图中建立的直角坐标系中,抛物线的解析式为y=﹣ ![]() +c且过顶点C(0,5)(长度单位:m)
+c且过顶点C(0,5)(长度单位:m)
(1)直接写出c的值;
(2)现因搞庆典活动,计划沿拱桥的台阶表面铺设一条宽度为1.5m的地毯,地毯的价格为20元/m2 , 求购买地毯需多少元?
(3)在拱桥加固维修时,搭建的“脚手架”为矩形EFGH(H、G分别在抛物线的左右侧上),并铺设斜面EG.已知矩形EFGH的周长为27.5m,求斜面EG的倾斜角∠GEF的度数.(精确到0.1°)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com