
 如图,△ABC是边长为6的等边三角形,以BC所在直线为x轴,BC的垂直平分线为y轴建立平面直角坐标系,点D为射线AO上任意一点(不与点A重合),以点D为圆心的圆始终与AB所在直线相切,在点D沿着射线AO平移的过程中,⊙D与x轴相切时,其半径为( )
如图,△ABC是边长为6的等边三角形,以BC所在直线为x轴,BC的垂直平分线为y轴建立平面直角坐标系,点D为射线AO上任意一点(不与点A重合),以点D为圆心的圆始终与AB所在直线相切,在点D沿着射线AO平移的过程中,⊙D与x轴相切时,其半径为( )| A. | $\sqrt{3}$ | B. | 3 | C. | $\sqrt{3}$或3$\sqrt{3}$ | D. | 2$\sqrt{3}$或3$\sqrt{3}$ |
分析 如图1,当⊙D与x轴相切时,且⊙D在x轴的上方,即⊙D是△ABC的内切圆,连接BD,由△ABC是边长为6的等边三角形,得到∠DBO=30°,BO=3,求得半径OD=BO•tan30°=$\sqrt{3}$;
如图2当⊙D与x轴相切时,且⊙D在x轴的下方,设⊙D与直线AB相切于E,连接DE,有△ABC是边长为6的等边三角形,得到∠EAD=30°,AO=3$\sqrt{3}$,∠AED=90°求得半径DE=3$\sqrt{3}$.
解答  解:如图1,当⊙D与x轴相切时,且⊙D在x轴的上方,
解:如图1,当⊙D与x轴相切时,且⊙D在x轴的上方,
即⊙D是△ABC的内切圆,
连接BD,
∵△ABC是边长为6的等边三角形,
∴∠DBO=30°,BO=3,
∴OD=BO•tan30°=$\sqrt{3}$;
如图2, 当⊙D与x轴相切时,且⊙D在x轴的下方,
当⊙D与x轴相切时,且⊙D在x轴的下方,
设⊙D与直线AB相切于E,连接DE,
∵△ABC是边长为6的等边三角形,
∴∠EAD=30°,AO=3$\sqrt{3}$,∠AED=90°
∴DE=$\frac{1}{2}$AD=$\frac{1}{2}$(3$\sqrt{3}$+DE),
∴DE=3$\sqrt{3}$,
∴⊙D的半径为;$\sqrt{3}$或3$\sqrt{3}$,
故选C.
点评 本题考查了切线的性质,坐标与图形的关系,等边三角形的性质,三角函数,正确的画出图形是解题的关键.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:填空题
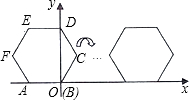 已知,正六边形ABCDEF在直角坐标系内的位置如图所示,A(-2,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2015次翻转之后,点B的坐标是(4031,$\sqrt{3}$).
已知,正六边形ABCDEF在直角坐标系内的位置如图所示,A(-2,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2015次翻转之后,点B的坐标是(4031,$\sqrt{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c+1=0的根的情况是( )
已知函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c+1=0的根的情况是( )| A. | 无实数根 | B. | 有两个相等实数根 | ||
| C. | 有两个异号实数根 | D. | 有两个同号不等实数根 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | p<m<n<q | B. | m<p<q<n | C. | m<p<n<q | D. | p<m<q<n |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=$\frac{1}{2}$x2+mx+n与直线y=-$\frac{1}{2}$x+3交于A,B两点,交x轴于D,C两点,连接AC,BC,已知A(0,3),C(3,0).
如图,抛物线y=$\frac{1}{2}$x2+mx+n与直线y=-$\frac{1}{2}$x+3交于A,B两点,交x轴于D,C两点,连接AC,BC,已知A(0,3),C(3,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com