
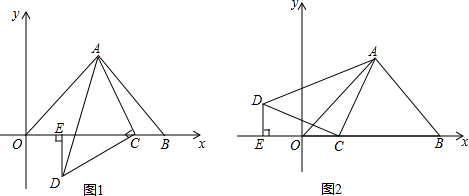
分析 (1)如图1中,作AM⊥OB垂足为M,只要证明△AMC≌△CED得AM=EC=4,利用线段和差定义即可解决.
(2)如图2中,作AM⊥OB垂足为M,只要证明△AMC≌△CED得AM=EC=4,利用线段和差定义即可解决.
解答 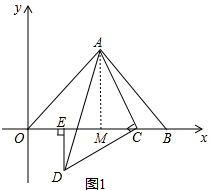 解;(1)如图1中,作AM⊥OB垂足为M.
解;(1)如图1中,作AM⊥OB垂足为M.
∵∠AMC=∠CED=∠ACD=90°,
∴∠ACM+∠DCE=90°,∠DCE+∠EDC=90°,
∴∠ACM=∠CDE,
在△AMC和△CED中,
$\left\{\begin{array}{l}{∠AMC=∠CED}\\{∠ACM=∠CDE}\\{AC=CD}\end{array}\right.$,
∴△AMC≌△CED,
∴AM=CE,
∵OA=AB,AM⊥OB,
∴AM=OM=MB=4,CE=AM=4,
∴OE=OB-EC-BC=8-4-t=4-t.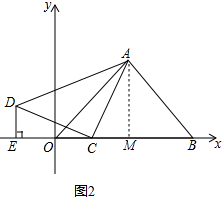
(2)如图2中,作AM⊥OB垂足为M.
∵∠AMC=∠CED=∠ACD=90°,
∴∠ACM+∠DCE=90°,∠DCE+∠EDC=90°,
∴∠ACM=∠CDE,
在△AMC和△CED中,
$\left\{\begin{array}{l}{∠AMC=∠CED}\\{∠ACM=∠CDE}\\{AC=CD}\end{array}\right.$,
∴△AMC≌△CED,
∴AM=CE,
∵OA=AB,AM⊥OB,
∴AM=OM=MB=4,CE=AM=4,
∴OE=EC-OC=EC-(OB-BC)=4-(8-t)=t+4.
点评 本题考查等腰三角形的性质、全等三角形的判定和性质、线段和差定义,添加辅助线寻找全等三角形是解决问题的关键.


 作业辅导系列答案
作业辅导系列答案科目:初中数学 来源:2017届广东省广州市九年级下学期3月月考数学试卷(解析版) 题型:单选题
将四根长度相等的细木条首尾相接,用钉子钉成四边形ABCD,转动这个四边形,使它形状改变,当∠B=90°时,如图①,测得AC=2,当∠B=60°时,如图②,AC=( ).

A.  B. 2 C.
B. 2 C.  D. 2
D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系中,抛物线C1:y=$\frac{1}{2}{x}^{2}$,把C1沿x轴向右平移m(m>0)个单位长度,得抛物线C2,C1和C2的交点为点Q,顶点分别是O和P,
在平面直角坐标系中,抛物线C1:y=$\frac{1}{2}{x}^{2}$,把C1沿x轴向右平移m(m>0)个单位长度,得抛物线C2,C1和C2的交点为点Q,顶点分别是O和P,查看答案和解析>>
科目:初中数学 来源:2016-2017学年江西省新余市八年级下学期第一次段考数学试卷(解析版) 题型:单选题
下列各式计算正确的是( )
A. 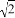 +
+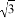 =
=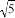 B. 4
B. 4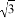 -3
-3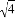 =1
=1
C. 2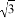 ×3
×3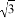 =6 D.
=6 D. 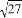 ÷
÷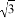 =3
=3
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com