
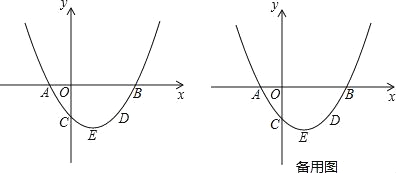
【题目】如图,已知在平面直角坐标系中,A,B两点在x轴上,线段OA,OB的长分别为方程x2-8x+12=0的两个根(OB>OA),点C是y轴上一点,其坐标为(0,-3).
(1)求A,B两点的坐标;
(2)求经过A,B,C三点的抛物线的关系式;
(3)D是点C关于该抛物线对称轴的对称点,E是该抛物线的顶点,M,N分别是y轴、x轴上的两个动点.
①当△CEM是等腰三角形时,请直接写出此时点M的坐标;
②以D、E、M、N位顶点的四边形的周长是否有最小值?若有,请求出最小值,并直接写出此时点M,N的坐标;若没有,请说明理由.
【答案】(1)A(-2,0),B(6,0)(2)y=![]() x2-x-3.(3)
x2-x-3.(3)![]() ,M(0,-
,M(0,-![]() ),N(
),N(![]() ,0).
,0).
【解析】
试题分析:(1)利用分解因式法解方程x2-8x+12=0即可得出x的值,再根据OB>OA即可得出点A、B的坐标;
(2)根据抛物线过x轴上的两点AB,可设抛物线的解析式为:y=a(x+2)(x-6)(a≠0),再由点C的坐标利用待定系数法即可求出经过A,B,C三点的抛物线的关系式;
(3)①设点M的坐标为(0,m),根据抛物线的关系式即可得出点E的坐标,由两点间的距离公式可求出线段CE、CM、ME的长度,再根据等腰三角形的性质分三种情况考虑,由边相等得出关于m的方程,解方程即可得出m值,从而得出点M的坐标;
②作点E关于y轴对称的点E′,作点D关于x轴对称的点D′,连接D′E′交x轴于点N,交y轴于点M,此时以D、E、M、N位顶点的四边形的周长最小.根据点C的坐标可得出点D的坐标,根据对称的性质即可得出点D′、E′的坐标,由此即可求出四边形周长的最小值,再根据点D′、E′的坐标,利用待定系数法即可求出直线D′E′的解析式,由此即可得出点M、N的坐标.
试题解析:(1)∵x2-8x+12=0,
∴(x-2)(x-6)=0,
解得:x1=2,x2=6,
∵OB>OA,
∴OA=2,OB=6,
∴点A的坐标为(-2,0),点B的坐标为(6,0).
(2)设抛物线的解析式为:y=a(x+2)(x-6)(a≠0),
将C(0,-3)代入得:-3=-12a,
解得:a=![]() ,
,
∴经过A,B,C三点的抛物线的关系式为:y=![]() (x+2)(x-6)=
(x+2)(x-6)=![]() x2-x-3.
x2-x-3.
(3)①依据题意画出图形,如图1所示.
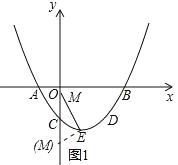
设点M的坐标为(0,m),
∵抛物线的关系式为y=![]() x2-x-3=
x2-x-3=![]() (x-2)2-4,
(x-2)2-4,
∴点E(2,-4),
∴CE=![]() ,CM=|m+3|,ME=
,CM=|m+3|,ME=![]() .
.
△CEM是等腰三角形分三种情况:
当CE=CM时,有![]() =|m+3|,
=|m+3|,
解得:m=![]() -3或m=-
-3或m=-![]() -3,
-3,
此时点M的坐标为(0,![]() -3)或(0,-
-3)或(0,-![]() -3);
-3);
当CE=ME时,有![]() =
=![]() ,
,
解得:m=-3(舍去)或m=-5,
此时点M的坐标为(0,-5);
当CM=ME时,有|m+3|=![]() ,
,
解得:m=-![]() ,
,
此时点M的坐标为(0,-![]() ).
).
综上可知:当△CEM是等腰三角形时,点M的坐标为(0,![]() -3)、(0,-
-3)、(0,-![]() -3)、(0,-5)或(0,-
-3)、(0,-5)或(0,-![]() ).
).
②四边形DEMN有最小值.
作点E关于y轴对称的点E′,作点D关于x轴对称的点D′,连接D′E′交x轴于点N,交y轴于点M,此时以D、E、M、N位顶点的四边形的周长最小,如图2所示.
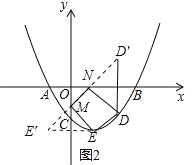
∵点C(0,-3),点E(2,-4),
∴点D(4,-3),DE=![]() .
.
∵E、E′关于y轴对称,D、D′关于x轴对称,
∴EM=E′M,DN=D′N,点E′(-2,-4),点D′(4,3),
∴EM+MN+DN=D′E′=![]() ,
,
∴C四边形DEMN=DE+EM+MN+DN=![]() .
.
设直线D′E′的解析式为y=kx+b,
则有![]() ,解得:
,解得: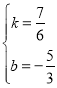 ,
,
∴直线D′E′的解析式为y=![]() x-
x-![]() .
.
令y=![]() x-
x-![]() 中x=0,则y=-
中x=0,则y=-![]() ,
,
∴点M(0,-![]() );
);
令y=![]() x-
x-![]() 中y=0,则
中y=0,则![]() x-
x-![]() =0,解得:x=
=0,解得:x=![]() ,
,
∴点N(![]() ,0).
,0).
故以D、E、M、N位顶点的四边形的周长有最小值,最小值为![]() ,此时点M的坐标为(0,-
,此时点M的坐标为(0,-![]() ),点N的坐标为(
),点N的坐标为(![]() ,0).
,0).


科目:初中数学 来源: 题型:
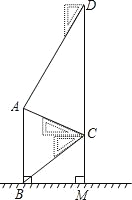
【题目】如图,某中学在教学楼前新建了一座雕塑AB.为了测量雕塑的高度,小明在二楼找到一点C,利用三角尺测得雕塑顶端点A的仰角为30°,底部点B的俯角为45°,小华在五楼找到一点D,利用三角尺测得点A的俯角为60°.若CD为9.6m,则雕塑AB的高度为多少?(结果精确到0.1m,参考数据:![]() ≈1.73).
≈1.73).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班抽取6名同学进行体育达标测试,成绩如下:80,90,75,80,75,80.下列关于对这组数据的描述错误的是( )
A. 中位数是75B. 平均数是80C. 众数是80D. 极差是15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查方式,你认为最合适的是
A. 日光灯管厂要检测一批灯管的使用寿命,采用全面调查方式
B. 旅客上飞机前的安检,采用抽样调查方式
C. 了解北京市居民日平均用水量,采用全面调查方式
D. 了解北京市每天的流动人口数,采用抽样调查方式
查看答案和解析>>
科目:初中数学 来源: 题型:
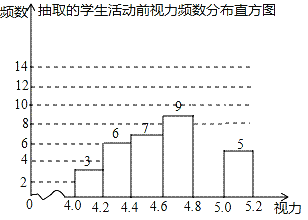
【题目】为了保护视力,学校计划开展“爱眼护眼”视力保健活动,为使活动更具有实效性,先对学生视力情况进行调查,随机抽取40名学生,检查他们的视力,并绘制不完整的直方图(数据包括左端点不包括右端点,精确到0.1),请结合直方图的信息解答下列问题:
(1)统计图中,4.8≤x<5.0的学生数是 人;
(2)将频数分布直方图补充完整;
(3)若绘制“学生视力扇形统计图”,视力达到4.8及以上为达标,则视为达标学生所对应扇形的圆心角度数为 °;
(4)若全校共有800名学生,则视力达标的学生估计有 名.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com