
【题目】某学校为了了解男生的体能情况,规定参加测试的每名男生从“实心球”,“立定跳远”,“引体向上”,“耐久跑1000米”四个项目中随机抽取一项作为测试项目.
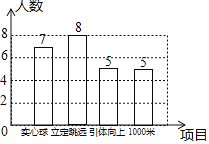
(1)八年(1)班的25名男生积极参加,参加各项测试项目的统计结果如图,参加“实心球”测试的男生人数是 人;
(2)八年(1)班有8名男生参加了“立定跳远”的测试,他们的成绩(单位:分)如下:95,100,82,90,89,90,90,85
①“95,100,82,90,89,90,90,85”这组数据的众数是 ,中位数是 .
②小聪同学的成绩是92分,他的成绩如何?
③如果将不低于90分的成绩评为优秀,请你估计八年级80名男生中“立定跳远”成绩为优秀的学生约为多少人?
【答案】(1)7;(2)①90;90;②小聪同学的成绩处于中等偏上;③有50人.
【解析】
(1)由统计结果图即可得出结果;
(2)①根据已知数据通过由小到大排列确定出众数与中位数即可;②求出8名男生成绩的平均数,然后用92与平均数进行比较即可;③求出成绩不低于90分占的百分比,乘以80即可得到结果.
(1)由统计结果图得:参加“实心球”测试的男生人数是7人,
故答案为:7;
(2)①将95,100,82,90,89,90,90,85这组数据由小到大排列:82,85,89,90,90,90,95,100;
根据数据得:众数为90,中位数为90,
故答案为:90;90;
②8名男生平均成绩为:![]() =90.125,
=90.125,
∵92>90.125,
∴小聪同学的成绩处于中等偏上;
③8名男生中达到优秀的共有5人,
根据题意得:![]() ×80=50(人),
×80=50(人),
则估计八年级80名男生中“立定跳远”成绩为优秀的学生约为50人.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】如图,线段AB是直线y=4x+2的一部分,点A是直线与y轴的交点,点B的纵坐标为6,曲线BC是双曲线y=![]() 的一部分,点C的横坐标为6,由点C开始不断重复“A﹣B﹣C”的过程,形成一组波浪线.点P(2017,m)与Q(2020,n)均在该波浪线上,分别过P、Q两点向x轴作垂线段,垂足为点D和E,则四边形PDEQ的面积是( )
的一部分,点C的横坐标为6,由点C开始不断重复“A﹣B﹣C”的过程,形成一组波浪线.点P(2017,m)与Q(2020,n)均在该波浪线上,分别过P、Q两点向x轴作垂线段,垂足为点D和E,则四边形PDEQ的面积是( )

A. 10 B. ![]() C.
C. ![]() D. 15
D. 15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的顶点 ![]() 在
在 ![]() 轴负半轴上,顶点
轴负半轴上,顶点![]() 在
在![]() 轴正半轴上,顶点
轴正半轴上,顶点 ![]() 在第一象限,线段
在第一象限,线段 ![]() ,
,![]() 的长是一元二次方程
的长是一元二次方程 ![]() 的两根,
的两根,![]() ,
,![]() .
.
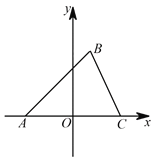
(1)直接写出点![]() 的坐标 点 C 的坐标 ;
的坐标 点 C 的坐标 ;
(2)若反比例函数![]() 的图象经过点
的图象经过点![]() ,求
,求 ![]() 的值;
的值;
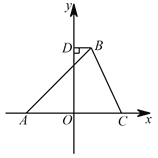
(3)如图过点![]() 作
作![]() 轴于点
轴于点 ![]() ;在
;在![]() 轴上是否存在点
轴上是否存在点 ![]() ,使以
,使以![]() ,
,![]() ,
,![]() 为顶点的三角形与以
为顶点的三角形与以![]() ,
,![]() ,
,![]() 为顶点的三角形相似?若存在,直接写出满足条件的点
为顶点的三角形相似?若存在,直接写出满足条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,完成后面题目.
0°-360°间的角的三角函数
在初中,我们学习过锐角的正弦、余弦、正切和余切四种三角函数,即在图1所示的直角三角形ABC,∠A是锐角,那么sinA=![]() ,cosA=
,cosA=![]() ,tanA=
,tanA=![]() ,cotA=
,cotA=![]()
为了研究需要,我们再从另一个角度来规定一个角的三角函数的意义:
设有一个角α,我们以它的顶点作为原点,以它的始边作为x轴的正半轴ox,建立直角坐标系(图2),在角α的终边上任取一点P,它的横坐标是x,纵坐标是y,点P和原点(0,0)的距离为r=![]() (r总是正的),然后把角α的三角函数规定为:sinα=
(r总是正的),然后把角α的三角函数规定为:sinα=![]() ,cosα=
,cosα=![]() ,tanα=
,tanα=![]() ,cotα=
,cotα=![]()
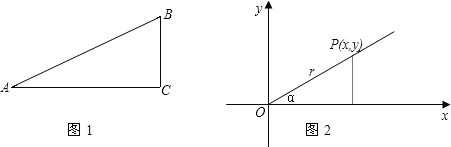
我们知道,图1的四个比值的大小与角A的大小有关,而与直角三角形的大小无关,同样图2中四个比值的大小也仅与角α的大小有关,而与点P在角α的终边位置无关.
比较图1与图2,可以看出一个角的三角函数的意义的两种规定实际上是一样的,根据第二种定义回答下列问题.
(1)若90°<α<180°,则角α的三角函数值sinα、cosα、tanα、cotα,其中取正值的是哪几个?
(2)若角α的终边与直线y=2x重合,求sinα+cosα的值.
(3)若角α是钝角,其终边上一点P(x,![]() ),且cosα=
),且cosα=![]() x,求tanα的值.
x,求tanα的值.
(4)若0°≤α≤90°,求sinα+cosα的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△A1B1C1中,A1B1=4,A1C1=5,B1C1=7.点A2,B2,C2分别是边B1C1,A1C1,A1B1的中点;点A3,B3,C3分别是边B2C2,A2C2,A2B2的中点;…;以此类推,则第2019个三角形的周长是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系xOy中,一次函数y=﹣![]() x+5的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,4).
x+5的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,4).
(1)求m的值及l2的解析式;
(2)求S△AOC﹣S△BOC的值;
(3)一次函数y=kx+1的图象为l3,且11,l2,l3不能围成三角形,直接写出k的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,△ABC各顶点都在格点上,点A,C的坐标分别为(﹣5,1)、(﹣1,4),结合所给的平面直角坐标系解答下列问题:
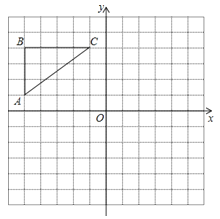
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)画出△ABC关于原点O对称的△A2B2C2;
(3)点C1的坐标是 ;点C2的坐标是 ;
(4)试判断:![]() 与
与![]() 是否关于x轴对称?(只需写出判断结果) .
是否关于x轴对称?(只需写出判断结果) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市2018年平均每天的垃圾处理量为40万吨/天,2019年平均每天的垃圾排放量比2018年平均每天的垃圾排放量多100万吨;2019年平均每天的垃圾处理量是2018年平均每天的垃圾处理量的2. 5倍. 若2019年平均每天的垃圾处理率是2018年平均每天的垃圾处理率的1. 25倍.
(注:![]() )
)
(1)求该市2018年平均每天的垃圾排放量;
(2)预计该市2020年平均每天的垃圾排放量比2019年平均每天的垃圾排放量增加![]() . 如果按照创卫要求“城市平均每天的垃圾处理率不低于
. 如果按照创卫要求“城市平均每天的垃圾处理率不低于![]() ”,那么该市2020年平均每天的垃圾处理量在2019年平均每天的垃圾处理量的基础上,至少还需要増加多少万吨才能使该市2020年平均每天的垃圾处理率符合创卫的要求?
”,那么该市2020年平均每天的垃圾处理量在2019年平均每天的垃圾处理量的基础上,至少还需要増加多少万吨才能使该市2020年平均每天的垃圾处理率符合创卫的要求?
查看答案和解析>>
科目:初中数学 来源: 题型:
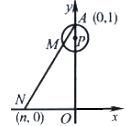
【题目】如图,在直角坐标系中,已知点A(0,1),点P在线段OA上,以AP为半径的⊙P周长为1.点M从A开始沿⊙P按逆时针方向转动,射线AM交x轴于点N(n,0),设点M转过的路程为m(0<m<1).随着点M的转动,当m从![]() 变化到
变化到![]() 时,点N相应移动的路径长为_______.
时,点N相应移动的路径长为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com