
【题目】某市为节约水资源,制定了新的居民用水收费标准,按照新标准,用户每月缴纳的水费y(元)与每月用水量x(m3)之间的关系如图所示. 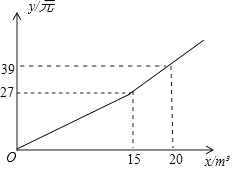
(1)求y关于x的函数解析式;
(2)若某用户二、三月份共用水40cm3(二月份用水量不超过25cm3),缴纳水费79.8元,则该用户二、三月份的用水量各是多少m3?
【答案】
(1)解:当0≤x≤15时,设y与x的函数关系式为y=kx,
15k=27,得k=1.8,
即当0≤x≤15时,y与x的函数关系式为y=1.8x,
当x>15时,设y与x的函数关系式为y=ax+b,
![]() ,得
,得 ![]() ,
,
即当x>15时,y与x的函数关系式为y=2.4x﹣9,
由上可得,y与x的函数关系式为y= ![]()
(2)解:设二月份的用水量是xm3,
当15<x≤25时,2.4x﹣9+2.4(40﹣x)﹣9=79.8,
解得,x无解,
当0<x≤15时,1.8x+2.4(40﹣x)﹣9=79.8,
解得,x=12,
∴40﹣x=28,
答:该用户二、三月份的用水量各是12m3、28m3
【解析】(1)根据函数图象可以分别设出各段的函数解析式,然后根据函数图象中的数据求出相应的函数解析式;(2)根据题意对x进行取值进行讨论,从而可以求得该用户二、三月份的用水量各是多少m3 .


科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,抛物线y=ax2+bx+2过点A(﹣3,0)、B (1,0),与y轴交于点C,抛物线的顶点为D,点G在抛物线上且其纵坐标为2.
(1)a= , b= , D( , ).
(2)P是线段AB上一动点(点P不与A、B重合),点P作x轴的垂线交抛物线于点E.
①若PE=PB,试求E点坐标;
②在①的条件下,PE、DG交于点M,在线段PE上是否存一点N,使得△DMN与△DCO相似?若存在,试求出相应点的坐标;
③在①的条件下,点F是坐标轴上一点,且点F到EC、ED的距离相等,试直接写出EF的长度.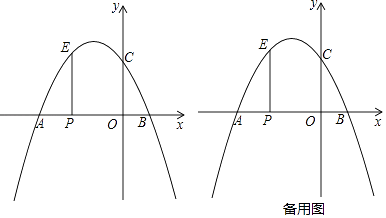
查看答案和解析>>
科目:初中数学 来源: 题型:
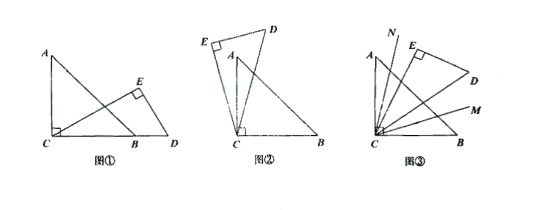
【题目】如图,将一个直角三角板中30°的锐角顶点与另一个直角三角板的直角顶点叠放一起.(注:∠ACB与∠DEC是直角,∠A=45°,∠DEC=30°).
(1)如图①,若点C、B、D在一条直线上,求∠ACE的度数;
(2)如图②,将直角三角板CDE绕点c逆时针方向转动到某个位置,若恰好平分∠DCE,求∠BCD的度数;
(3)如图③若∠DEC始终在∠ACB的内部,分别作射线CM平分∠BCD,射线CN平分∠ACE.如果三角板DCE在∠ACB内绕点C任意转动,∠MCN的度数是否发生变化?如果不变,求出它的度数,如果变化,说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DBE中,BC=BE,还需要添加两个条件才能使△ABC≌△DBE,则不能添加的一组条件是( )
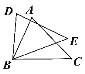
A. AC=DE,∠C=∠E B. BD=AB,AC=DE C. AB=DB,∠A=∠D D. ∠C=∠E,∠A=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE.
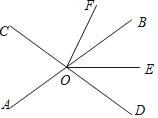
(1)若∠AOC=76°,求∠BOF的度数;
(2)若∠BOF=36°,求∠AOC的度数;
(3)若|∠AOC﹣∠BOF|=α°,请直接写出∠AOC和∠BOF的度数.(用含的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
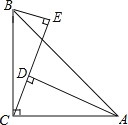
【题目】如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E.
(1)求证:△ACD≌△CBE;
(2)若AD=12,DE=7,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1=∠2,那么添加一个条件后,仍无法判定△ABD≌△ACD的是( )
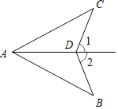
A. AB=AC B. ∠B=∠C C. AD平分∠CAB D. CD=BD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com