Question

平面内两条直线l₁∥l₂，它们之间的距离等于a．一块正方形纸板ABCD的边长也等于a．现将这块硬纸板如图所示放在两条平行线上．
（1）如图1，将点C放置在直线l₂上，且AC⊥l₁于O，使得直线l₁与AB、AD相交于E、F，证明：△AEF的周长等于2a；
请你继续完成下面的探索：
（2）如图2，若绕点C转动正方形硬纸板ABCD，使得直线l₁与AB、AD相交于E、F，试问△AEF的周长等于2a还成立吗？并证明你的结论；
（3）如图3，将正方形硬纸片ABCD任意放置，使得直线l₁与AB、AD相交于E、F，直线l₂与BC、CD相交于G，H，设△AEF的周长为m₁，△CGH的周长为m₂，试问m₁，m₂和a之间存在着什么关系？试证明你的结论．

Answer 1

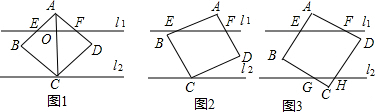
（1）证明：连接EC，FC．
∵AC⊥l₁，
∴∠B=∠COE=90°．
在Rt△BCE和Rt△OCE中
又∵BC=CO=a，EC=EC，
∴△BCE≌△OCE（HL）．
∴BE=EO．同理OF=FD．
∴AE+AF+EF=AB+AD=2a．

（2）如图4，过C作CM⊥EF于M，
则∠B=∠EMC=90°．
在Rt△BCE和Rt△MCE中，
∵BC=CM=a，EC=EC，
∴△BCE≌△MCE（HL），
同理△CMF≌△CDF
得BE=ME，MF=DF．
∴AE+AF+EF=AB+AD=2a．

（3）m₁+m₂=2a
证明：如图5将l₁，l₂分别同时向下平移相同的距离，则l₄和l₃的距离还是a，使得l₄经过点C，l₃交AB于M，交AD于N
由（2）的证明知AM+MN+AN=2a，
过F作FK∥AB交MN于K．
∴四边形EMKF为平行四边形．
∴EF=MK，FK=EM，
∵作FQ⊥MN于Q，CP⊥GH于P．则FQ=CP．
∵FK∥AB，
∴∠FKQ=∠AMN．
作BJ∥MN，
∴∠AMN=∠ABJ．
∵∠ABJ+∠CBJ=90°，∠CBJ=∠BGT=∠CGP，∠CGP+∠GHC=90°．
∴∠FKQ=∠GHC．
∴△FQK≌△CPH
∴FK=CH，KQ=PH．
同理FN=GC，NQ=GP．
∴KN=GH．则AE+AF+EF+GC+CH+GH，
=AE+EM+AF+FN+MK+KN，
=AM+AN+MN，
=2a．
分析：（1）首先连接EC，FC，根据△BCE≌△OCE，得出BE=EO以及OF=FD，进而得出AE+AF+EF=AB+AD的值；
（2）证明△BCE≌△MCE进而得出△CMF≌△CDF，得BE=ME，MF=DF，从而得出AE+AF+EF=AB+AD=2a；
（3）根据（2）中结论，以及平行四边形的性质得出FN=GC，NQ=GP，进而得出KN=GH，从从而求出AE+AF+EF+GC+CH+GH的值．
点评：此题主要考查了正方形的性质以及三角形全等的判定和平行线的性质等知识，利用三角形全等转化线段之间的等量关系是解决问题的关键．