
【题目】如图,Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于E,OD⊥BC交⊙O于D,DE交BC于F,点P为CB延长线上的一点,PE延长交AC于G,PE=PF,下列4个结论:①GE=GC;②AG=GE;③OG∥BE;④∠A=∠P.其中正确的结论是_____(填写所有正确结论的序号)
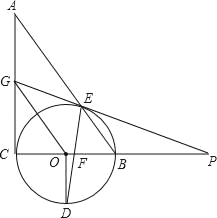
【答案】①②③
【解析】连接OE,CE,
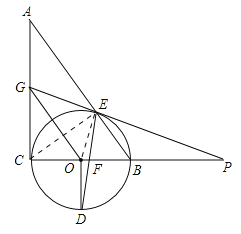
∵OE=OD,PE=PF,
∴∠OED=∠ODE,∠PEF=∠PFE,
∵OD⊥BC,
∴∠ODE+∠OFD=90°,
∵∠OFD=∠PFE,
∴∠OED+∠PEF=90°,
即OE⊥PE,
∵点E⊙O上,
∴PE为⊙O的切线;故①正确;
∵BC是直径,
∴∠BEC=90°,
∴∠AEC=90°
∵∠ACB=90°,
∴AC是⊙O的切线,
∴EG=CG,
∴∠GCE=∠GEC,
∵∠GCE+∠A=90°,∠GEC+∠AEG=90°,
∴∠A=∠AEG,
∴AG=EG,
∴AG=CG,
即G为AC的中点;故②正确;
∵OC=OB,
∴OG是△ABC的中位线,
∴OG∥AB,
即OG∥BE,故③正确;
在Rt△ABC中,∠A+∠ABC=90°,
在Rt△POE中,∠P+∠POE=90°,
∵OE=OB,
∴∠OBE=∠OEB,
但∠POE不一定等于∠ABC,
∴∠A不一定等于∠P.故④错误.
故答案为①②③.


 名师点拨卷系列答案
名师点拨卷系列答案科目:初中数学 来源: 题型:
【题目】“数形结合”是一种重要的数学思维,观察下面的图形和算式:
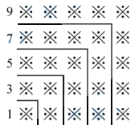
1=1=12
1+3=4=22
1+3+5=9=32
1+3+5+7=16=42
1+3+5+7+9=25=52
解答下列问题:请用上面得到的规律计算:21+23+25+27+…+101=( )
A.2601B.2501C.2400D.2419
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中xOy中,抛物线![]() 的顶点在x轴上.
的顶点在x轴上.
(1)求抛物线的表达式;
(2)点Q是x轴上一点,
①若在抛物线上存在点P,使得∠POQ=45°,求点P的坐标;
②抛物线与直线y=2交于点E,F(点E在点F的左侧),将此抛物线在点E,F(包含点E和点F)之间的部分沿x轴平移n个单位后得到的图象记为G,若在图象G上存在点P,使得∠POQ=45°,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,点![]() 在线段
在线段![]() 上,
上,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 的中点.求线段
的中点.求线段![]() 的长;
的长;
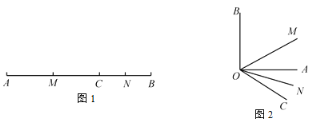
(2)点![]() 在线段
在线段![]() 上,若
上,若![]() ,点
,点![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 的中点.你能得出
的中点.你能得出![]() 的长度吗?并说明理由.
的长度吗?并说明理由.
(3)类似的,如图2,![]() 是直角,射线
是直角,射线![]() 在
在![]() 外部,且
外部,且![]() 是锐角,
是锐角,![]() 是
是![]() 的平分线,
的平分线,![]() 是
是![]() 的平分线.当
的平分线.当![]() 的大小发生改变时,
的大小发生改变时,![]() 的大小也会发生改变吗?为什么?
的大小也会发生改变吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于任意四个有理数a,b,c,d,可以组成两个有理数对(a,b)与(c,d).我们规定: (a,b)★(c,d)=bc-ad.例如:(1,2)★(3,4)=2×3-1×4=2.根据上述规定解决下列问题:
(1)有理数对(2,3)★(3,-2)= ;
(2)若有理数对(-3,2x-1)★(1,x+1)=12,则x= ;
(3)当满足等式(-3,2x-1)★(k,x+k)=3+2k的x是整数时,求整数k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由边长为1 的正方体搭成的立体图形,第(1)个图形由1个正方体搭成,第(2)个图形由4个正方体搭成,第(3)个图形由10个正方体搭成,以此类推,搭成第(6)个图形所需要的正方体个数是( )

A.84个B.56个C.37个D.36个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC沿射线BC向右平移到△DCE的位置,连接AD、BD,则下列结论:①AD=BC;②BD、AC互相平分;③四边形ACED是菱形.其中正确的个数是

A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上![]() 、
、![]() 两点分别表示有理数
两点分别表示有理数![]() 和
和![]() ,我们用
,我们用![]() 表示
表示![]() 到
到![]() 之间的距离;例如
之间的距离;例如![]() 表示7到3之间的距离.
表示7到3之间的距离.
(1)当![]() 时,
时,![]() 的值为 .
的值为 .
(2)如何理解![]() 表示的含义?
表示的含义?
(3)若点![]() 、
、![]() 在0到3(含0和3)之间运动,求
在0到3(含0和3)之间运动,求![]() 的最小值和最大值.
的最小值和最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为 __________________.
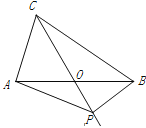
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com