

分析 (1)由已知得四边形ABCD为正方形,证明Rt△ADF≌Rt△ECD,然后推出∠ADE+∠DAF=90°;进而得出AF⊥DE;
(2)首先根据题意证明四边形MNPQ是菱形,然后又因为AF⊥DE,得出四边形MNPQ为正方形.
解答 解:(1)AF=DE,且AF⊥DE.理由如下:
∵四边形ABCD为正方形,
∴AD=DC=CB且∠ADC=∠DCB=90°,
在Rt△ADF和Rt△ECD中
$\left\{\begin{array}{l}{AD=DC}\\{∠ADC=∠DCB}\\{CE=DF}\end{array}\right.$,
∴Rt△ADF≌Rt△ECD(SAS),
∴AF=DE,
∴∠DAF=∠CDE,
∵∠ADE+∠CDE=90°,
∴∠ADE+∠DAF=90°,
∴∠AGD=90°,
∴AF⊥DE;
(2)结论:四边形MNPQ是正方形.
证明:∵AM=ME,AQ=QD,
∴MQ∥DE且MQ=$\frac{1}{2}$DE,
同理可证:PN∥DE,PN=$\frac{1}{2}$DE;MN∥AF,MN=$\frac{1}{2}$AF;PQ∥AF,PQ=$\frac{1}{2}$AF;
∵AF=DE,
∴MN=NP=PQ=QM,
∴四边形MNPQ是菱形,
又∵AF⊥DE,
∴∠MQP=90°,
∴四边形MNPQ是正方形.
点评 本题考查的是中点四边形,需要掌握全等三角形的判定,正方形的判定以及正方形的性质,难度一般.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,直线l1:y=-$\frac{1}{2}$x+6分别与x轴、y轴交于点B、C,且与直线l2:y=$\frac{1}{2}$x交于点A.
如图,在平面直角坐标系中,直线l1:y=-$\frac{1}{2}$x+6分别与x轴、y轴交于点B、C,且与直线l2:y=$\frac{1}{2}$x交于点A.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
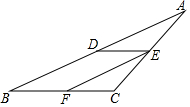 如图,已知DE∥BC,EF平分∠CED,∠A=∠CFE,那么EF与AB平行吗?为什么?
如图,已知DE∥BC,EF平分∠CED,∠A=∠CFE,那么EF与AB平行吗?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
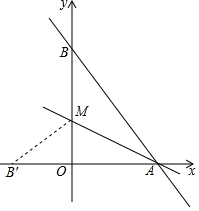 直线y=-$\frac{4}{3}$x+8与x轴、y轴分别交于点A和点B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则M的坐标为(0,3).
直线y=-$\frac{4}{3}$x+8与x轴、y轴分别交于点A和点B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则M的坐标为(0,3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com