
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:

| ||
| 14 |
| ||
| 14 |
查看答案和解析>>
科目:初中数学 来源:三点一测丛书九年级数学上 题型:059
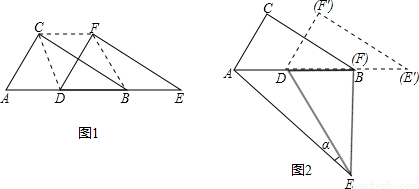
拿一张纸对折后,剪成两个全等的三角形,把这两个三角形一起放到图中△ABC的位置上.试一试,如果其中一个三角形不动,怎样移动另一个三角形,能够得到图中的各图形:

通过实际操作可以知道:(1)把△ABC沿直线BC移动线段BC那样长的距离,可以变到△ECD的位置;(2)以BC为轴把△ABC翻折![]() ,可以变到△DBC的位置;(3)以点A为中心,把△ABC旋转
,可以变到△DBC的位置;(3)以点A为中心,把△ABC旋转![]() ,可以变到△AED的位置.这些图形中的两个三角形之间有这样的关系,其中一个三角形是由另一个三角形按平行移动、翻折或旋转等方法得到的,像这样按一定方法把一个图形变成另一个图形叫做图形变换.
,可以变到△AED的位置.这些图形中的两个三角形之间有这样的关系,其中一个三角形是由另一个三角形按平行移动、翻折或旋转等方法得到的,像这样按一定方法把一个图形变成另一个图形叫做图形变换.
经过图形变换,图形的一些性质改变了,而另一些性质仍然保留下来.上面三个图形经过变换,图形的位置变化了,但形状大小都没有改变,即变换前后的图形全等,像这样只改变图形的位置,而不改变其形状大小的图形变换叫做全等变换.
利用图形变换,可以为研究几何图形提供方便.
试一试,你能用两个全等三角形拼成图中的各种图形吗?这些图形都可以看成是一个三角形经过全等变换得到的.

查看答案和解析>>
科目:初中数学 来源: 题型:044
(2004青岛课改)把两个全等的等腰直角三角板ABC和EFG(其直角边长均为4)叠放在一起(如图①),且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合.现将三角形板EFG绕O点按顺时针方向旋转(旋转角α满足条件:0°<α<90°),四边形CHGK是旋转过程中两三角板的重叠部分(如图②).
|
图① |
图② |
(1)在上述旋转过程中,BH与CK有怎样的数量关系?四边形CHGK的面积有何变化?证明你发现的结论;
(2)连接HK,在上述旋转过程中,设BH=x,△GKH的面积为y,求y与x之间的函数关系式,并写出自变量x的取值范围;
(3)在(2)的前提下,是否存在某一位置,使△GKH的面积恰好等于△ABC面积的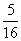 ?若存在,求出此时x的值;若不存在,说明理由.
?若存在,求出此时x的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源:2013年福建省泉州市惠安县初中学业质量检查数学试卷(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com