
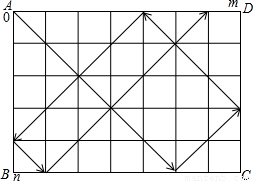
 证明:如图:将桌边的正方形顶点从A开始:
证明:如图:将桌边的正方形顶点从A开始:

 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
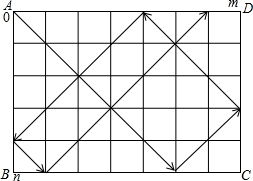
 17、一张台面为长方形ABCD的台球桌,只有四个角袋(分别以台面顶点A、B、C、D表示),台面的长、宽分别是m、n(m、n为互质的奇数,且m>n),台面被分成m×n个正方形.只用一个桌球,从桌角A以与桌边成45°夹角射出,碰到桌边后也以与桌边成45°角反弹(入射线与反射线垂直,如图).假设桌球不受阻力影响,在落袋前能一直运动.
17、一张台面为长方形ABCD的台球桌,只有四个角袋(分别以台面顶点A、B、C、D表示),台面的长、宽分别是m、n(m、n为互质的奇数,且m>n),台面被分成m×n个正方形.只用一个桌球,从桌角A以与桌边成45°夹角射出,碰到桌边后也以与桌边成45°角反弹(入射线与反射线垂直,如图).假设桌球不受阻力影响,在落袋前能一直运动.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图一张长正方形纸片ABCD,其长AD为a,宽AB为b(a>b),在BC边上选取一点E,将△ABE沿AE翻折后B至O的位置,若O为长方形纸片ABCD的对称中心,则
如图一张长正方形纸片ABCD,其长AD为a,宽AB为b(a>b),在BC边上选取一点E,将△ABE沿AE翻折后B至O的位置,若O为长方形纸片ABCD的对称中心,则| a |
| b |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com