
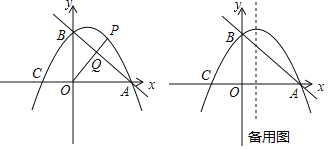
”¾ĢāÄæ”æČēĶ¼£¬Ö±Ļßy=©![]() x+3ÓėxÖį½»ÓŚµćA£¬ÓėyÖį½»ÓŚµćB£®Å×ĪļĻßy=©
x+3ÓėxÖį½»ÓŚµćA£¬ÓėyÖį½»ÓŚµćB£®Å×ĪļĻßy=©![]() x2+bx+c¾¹żA”¢BĮ½µć£¬ÓėxÖįµÄĮķŅ»øö½»µćĪŖC£®
x2+bx+c¾¹żA”¢BĮ½µć£¬ÓėxÖįµÄĮķŅ»øö½»µćĪŖC£®
£Ø1£©ĒóÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©µćPŹĒµŚŅ»ĻóĻŽÅ×ĪļĻßÉĻµÄµć£¬Į¬½ÓOP½»Ö±ĻßABÓŚµćQ£®ÉčµćPµÄŗį×ų±źĪŖm£¬PQÓėOQµÄ±ČÖµĪŖy£¬ĒóyÓėmµÄ¹ŲĻµŹ½£¬²¢Ēó³öPQÓėOQµÄ±ČÖµµÄ×ī“óÖµ£»
£Ø3£©µćDŹĒÅ×ĪļĻ߶Ō³ĘÖįÉĻµÄŅ»¶Æµć£¬Į¬½ÓOD”¢CD£¬Éč”÷ODCĶā½ÓŌ²µÄŌ²ŠÄĪŖM£¬µ±sin”ĻODCµÄÖµ×ī“óŹ±£¬ĒóµćMµÄ×ų±ź£®
”¾“š°ø”æ£Ø1£©Å×ĪļĻß½āĪöŹ½ĪŖy=©![]() x2+
x2+![]() x+3£»£Ø2£©y=©
x+3£»£Ø2£©y=©![]() m2+
m2+![]() m£¬PQÓėOQµÄ±ČÖµµÄ×ī“óÖµĪŖ
m£¬PQÓėOQµÄ±ČÖµµÄ×ī“óÖµĪŖ![]() £»£Ø3£©µćMµÄ×ų±źĪŖ£Ø©1£¬
£»£Ø3£©µćMµÄ×ų±źĪŖ£Ø©1£¬![]() £©»ņ£Ø©1£¬©
£©»ņ£Ø©1£¬©![]() £©£®
£©£®
”¾½āĪö”æ
£Ø1£©øł¾ŻÖ±Ļß½āĪöŹ½ĒóµĆµćA”¢BµÄ×ų±ź£¬½«Į½µćµÄ×ų±ź“śČėÅ×ĪļĻß½āĪöŹ½Ēó½āæÉµĆ£»
£Ø2£©¹żµćP×÷yÖįµÄĘ½ŠŠĻß½»ABÓŚµćE£¬¾Ż“ĖÖŖ”÷PEQ”×”÷OBQ£¬øł¾Ż¶ŌÓ¦±ß³É±ČĄżµĆy=![]() PE£¬ÓÉP£Øm£¬©
PE£¬ÓÉP£Øm£¬©![]() m2+
m2+![]() m+3£©”¢E£Øm£¬©
m+3£©”¢E£Øm£¬©![]() m+3£©µĆPE=©
m+3£©µĆPE=©![]() m2+
m2+![]() m£¬½įŗĻy=
m£¬½įŗĻy=![]() PEæɵĆŗÆŹż½āĪöŹ½£¬ĄūÓƶž“ĪŗÆŹżŠŌÖŹµĆĘä×ī“óÖµ£»
PEæɵĆŗÆŹż½āĪöŹ½£¬ĄūÓƶž“ĪŗÆŹżŠŌÖŹµĆĘä×ī“óÖµ£»
£Ø3£©ÉčCOµÄ“¹Ö±Ę½·ÖĻßÓėCO½»ÓŚµćN£¬ÖŖµćMŌŚCOµÄ“¹Ö±Ę½·ÖĻßÉĻ£¬Į¬½ÓOM”¢CM”¢DM£¬øł¾Ż”ĻODC=![]() ”ĻCMO=”ĻOMN”¢MC=MO=MDÖŖsin”ĻODC=sin”ĻOMN=
”ĻCMO=”ĻOMN”¢MC=MO=MDÖŖsin”ĻODC=sin”ĻOMN=![]() £¬µ±MDČ”×īŠ”ÖµŹ±£¬sin”ĻODC×ī“󣬾Ż“Ė½ųŅ»²½Ēó½āæÉµĆ£®
£¬µ±MDČ”×īŠ”ÖµŹ±£¬sin”ĻODC×ī“󣬾Ż“Ė½ųŅ»²½Ēó½āæÉµĆ£®
£Ø1£©ŌŚy=©![]() x+3ÖŠ£¬Įīy=0µĆx=4£¬Įīx=0µĆy=3£¬
x+3ÖŠ£¬Įīy=0µĆx=4£¬Įīx=0µĆy=3£¬
”ąµćA£Ø4£¬0£©”¢B£Ø0£¬3£©£¬
°ŃA£Ø4£¬0£©”¢B£Ø0£¬3£©“śČėy=©![]() x2+bx+c£¬µĆ£ŗ
x2+bx+c£¬µĆ£ŗ
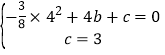 £¬
£¬
½āµĆ£ŗ![]() £¬
£¬
”ąÅ×ĪļĻß½āĪöŹ½ĪŖy=©![]() x2+
x2+![]() x+3£»
x+3£»
£Ø2£©ČēĶ¼1£¬¹żµćP×÷yÖįµÄĘ½ŠŠĻß½»ABÓŚµćE£¬
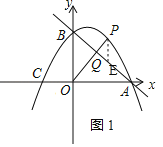
Ōņ”÷PEQ”×”÷OBQ£¬
”ą![]() £¬
£¬
”ß![]() =y”¢OB=3£¬
=y”¢OB=3£¬
”ąy=![]() PE£¬
PE£¬
”ßP£Øm£¬©![]() m2+
m2+![]() m+3£©”¢E£Øm£¬©
m+3£©”¢E£Øm£¬©![]() m+3£©£¬
m+3£©£¬
ŌņPE=£Ø©![]() m2+
m2+![]() m+3£©©£Ø©
m+3£©©£Ø©![]() m+3£©=©
m+3£©=©![]() m2+
m2+![]() m£¬
m£¬
”ąy=![]() £Ø©
£Ø©![]() m2+
m2+![]() m£©=©
m£©=©![]() m2+
m2+![]() m=©
m=©![]() £Øm©2£©2+
£Øm©2£©2+![]() £¬
£¬
”ß0£¼m£¼3£¬
”ąµ±m=2Ź±£¬y×ī“óÖµ=![]() £¬
£¬
”ąPQÓėOQµÄ±ČÖµµÄ×ī“óÖµĪŖ![]() £»
£»
£Ø3£©ČēĶ¼£¬ÓÉÅ×ĪļĻßy=©![]() x2+
x2+![]() x+3Ņ×ĒóC£Ø©2£¬0£©£¬¶Ō³ĘÖįĪŖÖ±Ļßx=1£¬
x+3Ņ×ĒóC£Ø©2£¬0£©£¬¶Ō³ĘÖįĪŖÖ±Ļßx=1£¬
”ß”÷ODCµÄĶāŠÄĪŖµćM£¬
”ąµćMŌŚCOµÄ“¹Ö±Ę½·ÖĻßÉĻ£¬
ÉčCOµÄ“¹Ö±Ę½·ÖĻßÓėCO½»ÓŚµćN£¬Į¬½ÓOM”¢CM”¢DM£¬

Ōņ”ĻODC=![]() ”ĻCMO=”ĻOMN”¢MC=MO=MD£¬
”ĻCMO=”ĻOMN”¢MC=MO=MD£¬
”ąsin”ĻODC=sin”ĻOMN=![]() £¬
£¬
ÓÖMO=MD£¬
”ąµ±MDČ”×īŠ”ÖµŹ±£¬sin”ĻODC×ī“ó£¬
“ĖŹ±”ŃMÓėÖ±Ļßx=1ĻąĒŠ£¬MD=2£¬
MN=![]() =
=![]() £¬
£¬
”ąµćM£Ø©1£¬©![]() £©£¬
£©£¬
øł¾Ż¶Ō³ĘŠŌ£¬ĮķŅ»µć£Ø©1£¬![]() £©Ņ²·ūŗĻĢāŅā£»
£©Ņ²·ūŗĻĢāŅā£»
×ŪÉĻĖłŹö£¬µćMµÄ×ų±źĪŖ£Ø©1£¬![]() £©»ņ£Ø©1£¬©
£©»ņ£Ø©1£¬©![]() £©£®
£©£®


 ½ĢѧĮ·ŠĀĶ¬²½Į·Ļ°ĻµĮŠ“š°ø
½ĢѧĮ·ŠĀĶ¬²½Į·Ļ°ĻµĮŠ“š°ø æĪĒ°æĪŗóĶ¬²½Į·Ļ°ĻµĮŠ“š°ø
æĪĒ°æĪŗóĶ¬²½Į·Ļ°ĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚÕż·½ŠĪABCDÖŠ£¬EŹĒBCµÄÖŠµć£¬FŹĒCDÉĻŅ»µć£¬AE”ĶEF£®ÓŠĻĀĮŠ½įĀŪ£ŗ¢Ł”ĻBAE£½30”ć£»¢ŚÉäĻßFEŹĒ”ĻAFCµÄ½ĒĘ½·ÖĻߣ»¢ŪAE2£½ADAF£»¢ÜAF£½AB+CF£®ĘäÖŠÕżČ·½įĀŪĪŖŹĒ______£®£ØĢīŠ“ĖłÓŠÕżČ·½įĀŪµÄŠņŗÅ£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijŠ£ĘßÄź¼¶¼Ę»®³ÉĮ¢Ń§ÉśÉēĶÅ£¬ŅŖĒóĆæŅ»Ī»Ń§Éś¶¼Ń”ŌńŅ»øöÉēĶŶųĒŅÖ»ÄÜŃ”ŌńŅ»øöÉēĶÅ£®ĪŖĮĖ½āѧɜ¶Ō²»Ķ¬ÉēĶŵÄŃ”ŌńŅāĻņ£¬Ė껜³éČ”ĮĖĘßÄź¼¶²æ·Öѧɜ½ųŠŠ”°ĪŅ×īĻ²°®µÄÉēĶÅ”±ĪŹ¾ķµ÷²é£¬²¢½«µ÷²é½į¹ū»ęÖĘ³ÉČēĻĀĮ½øö²»ĶźÕūµÄĶ³¼ĘĶ¼±ķ£®
ĘßÄź¼¶²æ·Öѧɜ”°ĪŅ×īĻ²°®µÄÉēĶÅ”±µ÷²é½į¹ūĶ³¼Ę±ķ
ÉēĶÅĆū³Ę | ČĖŹż |
ĪÄѧÉēĶÅ | 4 |
““æĶÉēĶÅ | 9 |
Źé·ØÉēĶÅ |
|
»ę»ÉēĶÅ | 6 |
ĢåÓżÉēĶÅ | 10 |
ŅōĄÖÉēĶÅ | 5 |
ĆĄŹ³ÉēĶÅ |
|
ŹżŃ§ÉēĶÅ | 2 |
ĘßÄź¼¶²æ·Öѧɜ”°ĪŅ×īĻ²°®µÄÉēĶÅ”±µ÷²é½į¹ūÉČŠĪĶ³¼ĘĶ¼
Ēė½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©![]() ______£¬
______£¬![]() ______£®
______£®
£Ø2£©ŌŚÉČŠĪĶ³¼ĘĶ¼ÖŠ£¬”°»ę»ÉēĶÅ”±Ėł¶ŌÓ¦µÄÉČŠĪŌ²ŠÄ½ĒĪŖ______¶Č£®
£Ø3£©øĆŠ£ĘßÄź¼¶¹²ÓŠ350Ćūѧɜ£¬ĆæøöÉēĶÅČĖŹż²»µĶÓŚ30ČĖ²ÅæÉŅŌæŖÕ¹£®ŹŌĶعż¼ĘĖć¹Ą¼ĘøĆŠ£ĘßÄź¼¶ÓŠÄÄŠ©ÉēĶÅæÉŅŌæŖÕ¹£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”ææĪĶāŌĶĮŹĒĢįøßѧɜĖŲŃųµÄÖŲŅŖĶ¾¾¶£®Ä³ÖŠŃ§ĪŖĮĖĮĖ½āČ«Š£Ń§ÉśæĪĶāŌĶĮĒéæö£¬Ė껜³é²éĮĖ200Ćūѧɜ£¬Ķ³¼ĘĖūĆĒĘ½¾łĆæĢģæĪĶāŌĶĮŹ±¼ä£ØŠ”Ź±£©£®øł¾ŻĆæĢģæĪĶāŌĶĮŹ±¼äµÄ³¤¶Ģ·ÖĪŖA£¬B£¬C£®DĖÄĄą£¬ĻĀĆęŹĒøł¾ŻĖł³é²éµÄČĖŹż»ęÖʵÄĮ½·ł²»ĶźÕūµÄĶ³¼ĘĶ¼±ķ£¬Ēėøł¾ŻĶ¼ÖŠĢį¹©µÄŠÅĻ¢£¬½ā“šĻĀĆęµÄĪŹĢā£ŗ
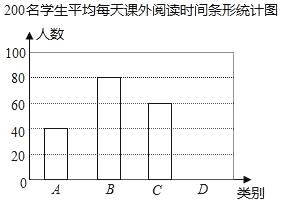
200ĆūŃ§ÉśĘ½¾łĆæĢģæĪĶāŌĶĮŹ±¼äĶ³¼Ę±ķ
Ąą±š | Ź±¼ät£ØŠ”Ź±£© | ČĖŹż |
A | t£¼0.5 | 40 |
B | 0.5”Üt£¼1 | 80 |
C | 1”Üt£¼1.5 | 60 |
D | t”Ż1.5 | a |
£Ø1£©Ēó±ķøńÖŠaµÄÖµ£¬²¢ŌŚĶ¼ÖŠ²¹Č«ĢõŠĪĶ³¼ĘĶ¼£ŗ
£Ø2£©øĆŠ£ĻÖÓŠ1800Ćūѧɜ£¬ĒėÄć¹Ą¼ĘøĆŠ£¹²ÓŠ¶ąÉŁĆūѧɜæĪĶāŌĶĮŹ±¼ä²»ÉŁÓŚ1Š”Ź±£æ
£Ø3£©ĒėÄćøł¾ŻÉĻŹöŠÅĻ¢¶ŌøĆŠ£Ģį³öĻąÓ¦µÄ½ØŅé
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĮõįēŹĒĪŅ¹ś¹Å“ś×ī½Ü³öµÄŹżŃ§¼ŅÖ®Ņ»£¬ĖūŌŚ”¶¾ÅĖćŹõŌ²ĢļŹõ£©ÖŠÓĆ”°øīŌ²Źõ”±Ö¤Ć÷ĮĖŌ²Ć껿µÄ¾«Č·¹«Ź½£¬²¢øų³öĮĖ¼ĘĖćŌ²ÖÜĀŹµÄæĘѧ·½·Ø£Ø×¢£ŗŌ²ÖÜĀŹ£½Ō²µÄÖܳ¤ÓėøĆŌ²Ö±¾¶µÄ±ČÖµ£©”°øīŌ²Źõ”±¾ĶŹĒŅŌ”°Ō²ÄŚ½ÓÕż¶ą±ßŠĪµÄĆ껿”±£¬Ą“ĪŽĻŽ±Ę½ü”°Ō²Ć껿”±£¬Įõ»ÕŠĪČŻĖūµÄ”°øīŌ²Źõ”±Ėµ£ŗøīÖ®ĆÖĻø£¬ĖłŹ§ĆÖÉŁ£¬øīÖ®ÓÖøī£¬ŅŌÖĮÓŚ²»æÉøī£¬ŌņÓėŌ²ŗĻĢ壬¶ųĪŽĖłŹ§ŅÓ£®Įõ»Õ¼ĘĖćŌ²ÖÜĀŹŹĒ“ÓÕżĮł±ßŠĪæŖŹ¼µÄ£¬Ņ×ÖŖŌ²µÄÄŚ½ÓÕżĮł±ßŠĪæÉ·ÖĪŖĮłøöČ«µČµÄÕżČż½ĒŠĪ£¬ĆæøöČż½ĒŠĪµÄ±ß³¤¾łĪŖŌ²µÄ°ė¾¶R£®“ĖŹ±Ō²ÄŚ½ÓÕżĮł±ßŠĪµÄÖܳ¤ĪŖ6R£¬Čē¹ū½«Ō²ÄŚ½ÓÕżĮł±ßŠĪµÄÖܳ¤µČĶ¬ÓŚŌ²µÄÖܳ¤£¬æɵĆŌ²ÖÜĀŹĪŖ3£®µ±ÕżŹ®¶ž±ßŠĪÄŚ½ÓÓŚŌ²Ź±£¬Čē¹ū°“ÕÕÉĻŹö·½·Ø¼ĘĖć£¬æɵĆŌ²ÖÜĀŹĪŖ_____£®£Ø²Īæ¼Źż¾Ż£ŗsinl5”ć£½0.26£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ![]() ÖŠ£¬
ÖŠ£¬![]() £¬ŅŌ
£¬ŅŌ![]() ĪŖÖ±¾¶×÷Ō²
ĪŖÖ±¾¶×÷Ō²![]() £¬·Ö±š½»
£¬·Ö±š½»![]() ÓŚµć
ÓŚµć![]() £¬½»
£¬½»![]() µÄŃÓ³¤ĻßÓŚµć
µÄŃÓ³¤ĻßÓŚµć![]() £¬¹żµć
£¬¹żµć![]() ×÷
×÷![]() ÓŚµć
ÓŚµć![]() £¬Į¬½Ó
£¬Į¬½Ó![]() ½»Ļ߶Ī
½»Ļ߶Ī![]() ÓŚµć
ÓŚµć![]() £®
£®
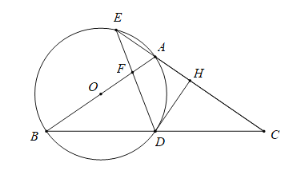
£Ø1£©ĒóÖ¤£ŗ![]() ŹĒŌ²
ŹĒŌ²![]() µÄĒŠĻߣ»
µÄĒŠĻߣ»
£Ø2£©Čō![]() ĪŖ
ĪŖ![]() µÄÖŠµć£¬Ēó
µÄÖŠµć£¬Ēó![]() µÄÖµ£»
掙术
£Ø3£©Čō![]() £¬ĒóŌ²
£¬ĒóŌ²![]() µÄ°ė¾¶£®
µÄ°ė¾¶£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”抔Ć÷ŌŚÉĻѧµÄĀ·ÉĻŅŖ¾¹ż¶ąøöĀ·æŚ£¬ĆæøöĀ·æŚ¶¼ÉčÓŠŗģ”¢»Ę”¢ĀĢČżÖÖŠÅŗÅµĘ£¬¼ŁÉčŌŚø÷Ā·æŚÓöµ½ŠÅŗÅµĘŹĒĻą»„¶ĄĮ¢µÄ.
(1).Čē¹ūÓŠ2øöĀ·æŚ£¬ĒóŠ”Ć÷ŌŚÉĻѧĀ·ÉĻµ½µŚ¶žøöĀ·æŚŹ±µŚŅ»“ĪÓöµ½ŗģµĘµÄøÅĀŹ£®£ØĒėÓĆ”°»Ź÷דĶ¼”±»ņ”°ĮŠ±ķ”±µČ·½·ØŠ“³ö·ÖĪö¹ż³Ģ£©
(2).Čē¹ūÓŠnøöĀ·æŚ£¬ŌņŠ”Ć÷ŌŚĆæøöĀ·æŚ¶¼Ć»ÓŠÓöµ½ŗģµĘµÄøÅĀŹŹĒ .
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻß![]() µÄ¶„µćĪŖ
µÄ¶„µćĪŖ![]() £¬½»
£¬½»![]() ÖįÓŚµć
ÖįÓŚµć![]() £¬
£¬![]() £Øµć
£Øµć![]() ŌŚµć
ŌŚµć![]() µÄÓŅ²ą£©£¬µć
µÄÓŅ²ą£©£¬µć![]() ŌŚµŚŅ»ĻóĻŽ£¬ĒŅŌŚÅ×ĪļĻß
ŌŚµŚŅ»ĻóĻŽ£¬ĒŅŌŚÅ×ĪļĻß![]() ²æ·ÖÉĻ£¬
²æ·ÖÉĻ£¬![]() ½»
½»![]() ÖįÓŚµć
ÖįÓŚµć![]() £®
£®
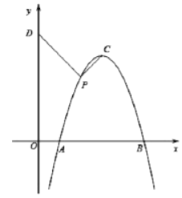
£Ø1£©ĒóøĆÅ×ĪļĻߵıķ“ļŹ½£®
£Ø2£©Čō![]() £¬Ēó
£¬Ēó![]() µÄ³¤£®
µÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
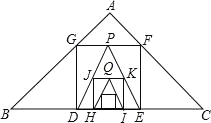
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖŌŚRt”÷ABCÖŠ£¬AB£½AC£½3![]() £¬ŌŚ”÷ABCÄŚ×÷µŚŅ»øöÄŚ½ÓÕż·½ŠĪDEFG£»Č»ŗóČ”GFµÄÖŠµćP£¬Į¬½ÓPD”¢PE£¬ŌŚ”÷PDEÄŚ×÷µŚ¶žøöÄŚ½ÓÕż·½ŠĪHIKJ£»ŌŁČ”Ļ߶ĪKJµÄÖŠµćQ£¬ŌŚ”÷QHIÄŚ×÷µŚČżøöÄŚ½ÓÕż·½ŠĪ”ŅĄ“Ī½ųŠŠĻĀČ„£¬ŌņµŚ2014øöÄŚ½ÓÕż·½ŠĪµÄ±ß³¤ĪŖ____£®
£¬ŌŚ”÷ABCÄŚ×÷µŚŅ»øöÄŚ½ÓÕż·½ŠĪDEFG£»Č»ŗóČ”GFµÄÖŠµćP£¬Į¬½ÓPD”¢PE£¬ŌŚ”÷PDEÄŚ×÷µŚ¶žøöÄŚ½ÓÕż·½ŠĪHIKJ£»ŌŁČ”Ļ߶ĪKJµÄÖŠµćQ£¬ŌŚ”÷QHIÄŚ×÷µŚČżøöÄŚ½ÓÕż·½ŠĪ”ŅĄ“Ī½ųŠŠĻĀČ„£¬ŌņµŚ2014øöÄŚ½ÓÕż·½ŠĪµÄ±ß³¤ĪŖ____£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com