
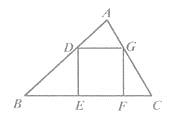
【题目】如图,△ABC中,正方形DEFG的顶点D,G分别在AB,AC上,顶点E,F在BC上.若△ADG、△BED、△CFG的面积分别是1、3、1,则正方形的边长为( )
A. ![]() B.
B. ![]() C. 2 D. 2
C. 2 D. 2![]()
科目:初中数学 来源: 题型:
【题目】新定义:对于关于x的一次函数y=kx+b(k≠0),我们称函数y=![]() 为一次函数y=kx+b(k≠0)的m变函数(其中m为常数).
为一次函数y=kx+b(k≠0)的m变函数(其中m为常数).
例如:对于关于x的一次函数y=x+4的3变函数为y=![]()
(1)关于x的一次函数y=-x+1的2变函数为![]() ,则当x=4时,
,则当x=4时,![]() = ;
= ;
(2)关于x的一次函数y=x+2的1变函数为![]() ,关于x的一次函数y=-
,关于x的一次函数y=-![]() x-2的-1变函数为
x-2的-1变函数为![]() ,求函数
,求函数![]() 和函数
和函数![]() 的交点坐标;
的交点坐标;
(3)关于x的一次函数y=2x+2的1变函数为![]() ,关于x的一次函数y=
,关于x的一次函数y=![]() x-1,的m变函数为
x-1,的m变函数为![]() .
.
①当-3≤x≤3时,函数![]() 的取值范围是 (直接写出答案):
的取值范围是 (直接写出答案):
②若函数![]() 和函数
和函数![]() 有且仅有两个交点,则m的取值范围是 (直接写出答案).
有且仅有两个交点,则m的取值范围是 (直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”黄金周期间,某市在![]() 天中外出旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
天中外出旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
日期 |
|
|
|
|
|
|
|
人数变化(万人) |
|
|
|
|
|
|
|
(1)若![]() 月
月![]() 日外出旅游人数为
日外出旅游人数为![]() ,那么
,那么![]() 月
月![]() 日外出旅游的人数是多少?
日外出旅游的人数是多少?
(2)请判断七天内外出旅游人数最多的是哪天?最少的是哪天?它们相差多少?
(3)如果最多一天有出游人数![]() 万人,那么若
万人,那么若![]() 月
月![]() 日外出旅游的有多少人?
日外出旅游的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
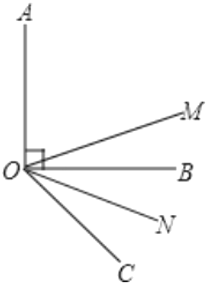
【题目】如图,已知![]() 与
与![]() 互为余角,且
互为余角,且![]() 平分
平分![]() 平分
平分![]() .
.
(1)求![]() 的度数;
的度数;
(2)如果已知![]() ,其他条件不变,则
,其他条件不变,则![]() _______度;如果已知
_______度;如果已知![]() ,其他条件不变,则
,其他条件不变,则![]() _______度;
_______度;
(3)从以上求![]() 的过程中,你得出的结论是__________.
的过程中,你得出的结论是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的情景对话,然后解答问题:
老师:我们新定义一种三角形,两边平方和等于第三边平方的2倍的三角形叫做奇异三角形.
小明:那直角三角形是否存在奇异三角形呢?
小红:等边三角形一定是奇异三角形.
(1)根据“奇异三角形”的定义,小红得出命题:“等边三角形一定是奇异三角形”,则小红提出的命题是 .(填“真命题”或“假命题”)
(2)若![]() 是奇异三角形,其中两边的长分别为
是奇异三角形,其中两边的长分别为![]() 、
、![]() ,则第三边的长为 .
,则第三边的长为 .
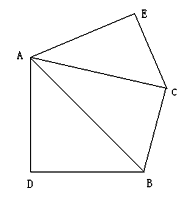
(3)如图,![]() 中,
中,![]() ,以
,以![]() 为斜边作等腰直角三角形
为斜边作等腰直角三角形![]() ,点
,点![]() 是
是![]() 上方的一点,且满足
上方的一点,且满足![]() .求证:
.求证:![]() 是奇异三角形.
是奇异三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】建设银行的某储蓄员小张在办理业务时,约定存入为正,取出为负. 2019年10月29日,他先后办理了七笔业务: +2000元、-800元、+400元、-800元、+1400元、-1700元、-200元.
(1)若他早上领取备用金4000元,那么下班时应交回银行_________元钱.
(2)请判断在这七次办理业务中,小张在第_______次业务办理后手中现金最多,第_________次业务办理后手中现金最少.
(3)若每办一件业务,银行发给业务量的0.2%作为奖励,小张这天应得奖金多少元?
(4)若记小张第一次办理业务前的现金为0点,用折线统计图表示这7次业务办理中小张手中现金的变化情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市共有一中、二中、三中等3所高中,有一天所有高二学生参加了一次数学测试,阅卷后老师们对第10题进行了分析,把每个学生的解答情况归结为下列四类情况之一:A(概念错误),B(计算错误),C(基本正确),D(完全正确).各校出现这四类情况的人数占本校高二学生数的百分比见下面的条形统计图:
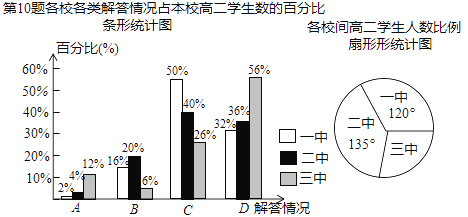
已知一中高二学生有400名,这三所学校之问高二学生人数的比例见扇形统计图.
(1)求全市高二学生总数;
(2)求全市解答完全正确的高二学生数占高二学生总数的百分比;
(3)请你对三中高二数学老师提一个值得关注的教学建议,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,2)与(0,3)之间(不包括这两点),对称轴为直线x=2.下列结论:abc<0;②9a+3b+c>0;③若点M(![]() ,y1),点N(
,y1),点N(![]() ,y2)是函数图象上的两点,则y1<y2;④﹣
,y2)是函数图象上的两点,则y1<y2;④﹣![]() <a<﹣
<a<﹣![]() .其中正确结论有( )
.其中正确结论有( )
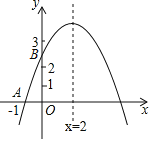
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小泽和小超分别用掷A、B两枚骰子的方法来确定P(x,y)的位置,她们规定:小泽掷得的点数为x,小超掷得的点数为![]() ,那么,她们各掷一次所确定的点落在已知直线y=-2x+6上的概率为( )
,那么,她们各掷一次所确定的点落在已知直线y=-2x+6上的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com