
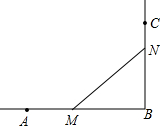
 如图,已知AB⊥BC,AB=12cm,BC=8cm.一只蝉从点C沿CB方向以1cm/s的速度爬行,一只螳螂为了捕捉这只蝉,由点A沿AB方向以2cm/s的速度爬行,一段时间后,它们分别到达了点M,N的位置.若此时△MNB的面积为24cm2,求它们爬行的时间.
如图,已知AB⊥BC,AB=12cm,BC=8cm.一只蝉从点C沿CB方向以1cm/s的速度爬行,一只螳螂为了捕捉这只蝉,由点A沿AB方向以2cm/s的速度爬行,一段时间后,它们分别到达了点M,N的位置.若此时△MNB的面积为24cm2,求它们爬行的时间. 分析 设它们爬行的时间为ts,则BM=12-2t,BN=8-t,根据△MNB的面积为24cm2,即可得出关于t的一元二次方程,解方程即可得出t的值,再将t的值代入12-2t中即可确定t的值,此题得解.
解答 解:设它们爬行的时间为ts,则BM=12-2t,BN=8-t,
∵△MNB的面积为24cm2,
∴$\frac{1}{2}$•(12-2t)•(8-t)=24,整理得:t2-14t+24=0,
解得:t1=2,t2=12.
当t=12时,12-2t=-12<0,
∴t=12不合适.
答:它们爬行的时间为2s.
点评 本题考查了一元二次方程的应用,根据数量关系列出关于t的一元二次方程是解题的关键.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{2}{b^2}$ | B. | 3b2 | C. | $-\frac{3}{2}{b^2}$ | D. | -3b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
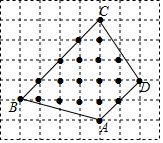 我们在计算不规则图形的面积时,有时采用“方格法”来计算.计算方法如下:假定每个小方格的边长为1个单位长度.S为图形的面积,L是边界上的格点数,N是内部格点数,则有S=$\frac{L}{2}$+N-1.请根据此方法计算图中四边形ABCD的面积.
我们在计算不规则图形的面积时,有时采用“方格法”来计算.计算方法如下:假定每个小方格的边长为1个单位长度.S为图形的面积,L是边界上的格点数,N是内部格点数,则有S=$\frac{L}{2}$+N-1.请根据此方法计算图中四边形ABCD的面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com