
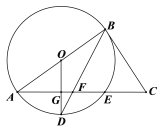
【题目】如图,在⊙O中,AB是⊙O的直径,AE是弦,OG⊥AE于点G,交⊙O 于点D,连结BD交AE于点F,延长AE至点C,连结BC.
(1)当BC=FC时,证明:BC是⊙O的切线;
(2)已知⊙O的半径![]() ,当tanA=
,当tanA=![]() ,求GF的长.
,求GF的长.
【答案】(1)见解析;(2)1
【解析】
(1)由OD⊥AE可知∠D+∠GFD=90°,由等腰三角形的性质可得∠BFC=∠FBC,∠OBD=∠D,从而可证∠OBC=90°;
(2) 连接 BE,在Rt△AOG中,可求出OG= 3, AG=4,由垂径定理得GE= AG=4,然后通过证明△FGD∽△FEB,可求出GF的长.
(1)证明:∵OD⊥AE.
∴∠D+∠GFD=90°.
∵BC=FC,
∴∠BFC=∠FBC.
∵∠BFC=∠GFD,
∴∠GFD=∠FBC.
∵OB=OD,
∴∠OBD=∠D.
∴∠OBD+∠CBF=∠D+∠GFD=90°.
即∠OBC=90°.
∴BC是![]() 的切线.
的切线.
(2) 连接 BE,

∵⊙O半径![]() ,tanA=
,tanA=![]() ,
,
∴sinA=![]() ,cosA=
,cosA=![]() .
.
∴在Rt△AOG中,OG=OA sinA=5×![]() =3, AG=OA cosA=5×
=3, AG=OA cosA=5×![]() =4=GE.
=4=GE.
∴GD=OD-OG=5-3=2.
∵OG⊥AE,
∴AG=GE.
∴OG是△ABE的中位线,
∴BE=2OG=6,BE∥OD.
∴∠D=∠FBE,∠BEF=∠FGD.
∴△FGD∽△FEB.
∴![]() .
.
∴![]() .
.
∴GF=1.


 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
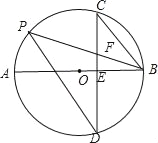
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,弦PB与CD交于点F,且FC=FB.
(1)求证:PD∥CB;
(2)若AB=26,EB=8,求CD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
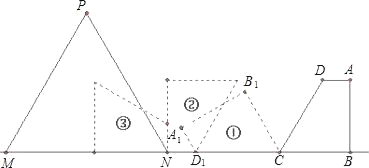
【题目】如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,BC=5,CD=6,∠DCB=60°,等边△PMN(N为固定点)的边长为x,边MN在直线BC上,NC=8.将直角梯形ABCD绕点C按逆时针方向旋转到①的位置,再绕点D1按逆时针方向旋转到②的位置,如此旋转下去.
(1)将直角梯形按此方法旋转四次,如果等边△PMN的边长为x≥5+3![]() ,求梯形与等边三角形的重叠部分的面积;
,求梯形与等边三角形的重叠部分的面积;
(2)将直角梯形按此方法旋转三次,如果梯形与等边三角形的重叠部分的面积是![]() ,求等边△PMN的边长x的范围.
,求等边△PMN的边长x的范围.
(3)将直角梯形按此方法旋转三次,如果梯形与等边三角形的重叠部分的面积是梯形面积的一半,求等边△PMN的边长x.
查看答案和解析>>
科目:初中数学 来源: 题型:
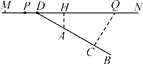
【题目】如图,MN表示一段笔直的高架道路,线段AB表示高架道路旁的一排居民楼,已知点A到MN的距离为15米,BA的延长线与MN相交于点D,且∠BDN=30°,假设汽车在高速道路上行驶时,周围39米以内会受到噪音(XRS)的影响.
(1)过点A作MN的垂线,垂足为点H,如果汽车沿着从M到N的方向在MN上行驶,当汽车到达点P处时,噪音开始影响这一排的居民楼,那么此时汽车与点H的距离为多少米?
(2)降低噪音的一种方法是在高架道路旁安装隔音板,当汽车行驶到点Q时,它与这一排居民楼的距离QC为39米,那么对于这一排居民楼,高架道路旁安装的隔音板至少需要多少米长?(精确到1米)(参考数据:![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行数学竞赛,对获一等奖的学生奖励数学家的著作《好玩的数学》,对获二等奖的学生奖励创意学生笔记本,若网购《好玩的数学》14元/本,创意学生笔记本12元/本,若《好玩的数学》数量比创意学生笔记本的数量的一半多5本,买两种奖品共用了1020元,购买两种奖品的数量各是多少本?

查看答案和解析>>
科目:初中数学 来源: 题型:
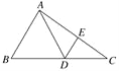
【题目】如图,已知△ABC中,点D在边BC上,∠DAB=∠B,点E在边AC上,满足AE·CD=AD·CE.
(1)求证:DE∥AB;
(2)如果点F是DE延长线上一点,且BD是DF和AB的比例中项,连接AF.求证:DF=AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
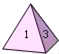
【题目】如图,均匀的正四面体的各面依次标有1,2,3,4四个数字.小明做了60次投掷试验,结果统计如下:
朝下数字 | 1 | 2 | 3 | 4 |
出现的次数 | 16 | 20 | 14 | 10 |
(1)计算上述试验中“4朝下”的频率是 ;
(2)随机投掷正四面体两次,请用列表或画树状图法,求两次朝下的数字之和大于4的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
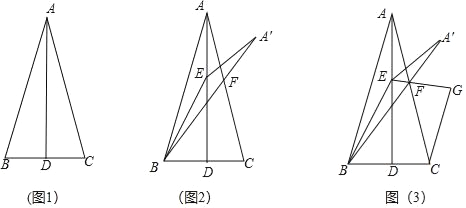
【题目】已知:AD是△ABC的高,且BD=CD.
(1)如图1,求证:∠BAD=∠CAD;
(2)如图2,点E在AD上,连接BE,将△ABE沿BE折叠得到△A′BE,A′B与AC相交于点F,若BE=BC,求∠BFC的大小;
(3)如图3,在(2)的条件下,连接EF,过点C作CG⊥EF,交EF的延长线于点G,若BF=10,EG=6,求线段CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
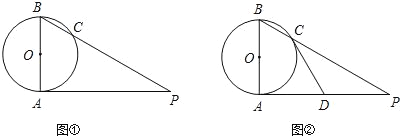
【题目】已知AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.
(1)如图①,若∠P=35°,求∠ABP的度数;
(2)如图②,若D为AP的中点,求证:直线CD是⊙O的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com