练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．已知单项式9am+1bn+1与-2a2m-1b2n-1的积与5a3b6是同类项，求mn的值（　　）
    A．4B．3C．2D．1

    分析 直接利用单项式乘以单项式运算性质得出关于m，n的等式，进而求出m，n的值，进而得出答案．

    解答 解：∵单项式9am+1bn+1与-2a2n-1b2n-1的积与5a3b6是同类项，
    ∴$\left\{\begin{array}{l}{m+1+2n-1=3}\\{n+1=2n-1}\end{array}\right.$，
    解得：$\left\{\begin{array}{l}{m=-1}\\{n=2}\end{array}\right.$，
    故mn=（-1）2=1．
    故选：D．

    点评 此题主要考查了单项式乘以单项式运算，正确掌握运算法则是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    5．在实数-2、0、2、3中，绝对值最小的实数是（　　）
    A．-2B．0C．2D．3

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．下列各组线段中，能组成三角形的是（　　）
    A．a=3cm，b=8cm，c=5cmB．a=12cm，b=5cm，c=6cm
    C．a=5cm，b=5cm，c=10cmD．a=15cm，b=10cm，c=7cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．下列图形中，是轴对称图形，不是中心对称图形的是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

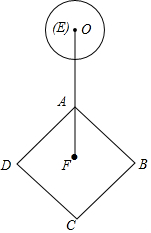    4．如图，边长为4cm的正方形ABCD，点F为正方形的中点，点E在FA的延长线上，EA=4cm，⊙O的半径为1cm，圆心O从点E出发向点F运动，小明发现：当EO满足①3＜EO＜5；②3≤EO≤5；③EO=4+$\sqrt{2}$；④EO=4+$3\sqrt{2}$时，⊙O与正方形ABCD的边只有两个公共点，你认为小明探究的结论中正确的有（　　）
    A．①③B．②③C．②④D．①③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

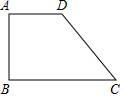    14．如图，梯形ABCD中，∠ABC=∠BAD=90°，AD=AB=1，∠BCD=45°．将梯形ABCD折叠，使得点C与点A重合，折痕交CD于E，交BC于F，画出图形．求出折叠后重叠部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．我区课堂教学改革已取得了阶段性成果，某校对八年级4个实验班、10个对比班（每班50人）进行了一次数学学科素养检测，分别抽取50名学生的成绩进行分析，并将结果绘制成如下统计表及统计图（数据包括左端点但不包括右端点，且收集的数据为整数）．
    （1）补全实验班检测结果频数分布直方图；
    （2）若检测成绩80分以上为优秀，试估计全校八年级学生中优秀学生约有多少人？
    （3）通过以上分析结果，小可同学认为实验班学生的平均分更高，你的看法呢？说说你的理由．

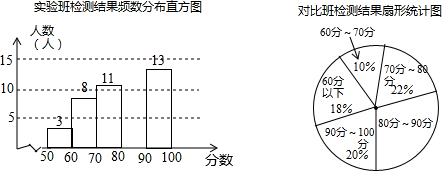
    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

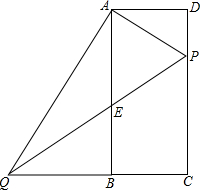    18．已知矩形ABCD中，AD=6，AB=12，P为边CD上的动点，过A点作AQ⊥AP，交CB的延长线于点Q，交AB于点E，若DP=x，CQ=y，
    （1）试写出y与x的函数关系式．
    （2）当x为何值时，△APE为等腰直角三角形？
    （3）直接写出P点由D向C运动过程中，PQ的中点F运动的路径的长？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．【问题提出】
    我们借助学习“图形的判定”获得的经验与方法对“平行四边形的判定”进一步探究．

    【初步思考】
    在一个四边形中，我们把“一组对边平行、一组对边相等、一组对角相等或一条对角线被另一条对角线平分”称为一个条件．如图1，四边形ABCD中，我们用符号语言表示出所有的8个条件：
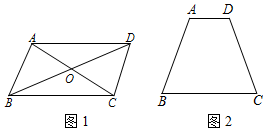
    ①AB=CD；②AD=BC；③AB∥CD；④AD∥BC；
    ⑤∠BAD=∠BCD；⑥∠ABC=∠ADC；⑦OA=OC；⑧OB=OD．
    那么满足2个条件的四边形是不是平行四边形呢？
    【深入探究】
    小莉所在学习小组进行了研究，她们认为2个条件可分为以下六种类型：
    Ⅰ关于对边的2个条件；Ⅱ关于对角的2个条件；
    Ⅲ关于对角线的2个条件；Ⅳ关于边的条件与角的条件各1个；
    Ⅴ关于边的条件与对角线的条件各1个；Ⅵ关于角的条件与对角线的条件各1个．
    （1）小明认为“Ⅰ关于对边的2个条件”可分为“①②，③④，①③，①④”共4种不同种类的情形．请你仿照小明的叙述对其它五种类型进一步分类．
    （2）小红认为有4种情形是平行四边形的判定依据．请你写出其它的三个判定定理．
    定义：两组对边分别平行的四边形是平行四边形；
    定理1：两组对边分别相等的四边形是平行四边形；
    定理2：一组对边平行且相等的四边形是平行四边形；
    定理3：对角线互相平分的四边形是平行四边形．
    （3）小刚认为除了4个判定依据外，还存在一些真命题，他写出了其中的1个，请证明这个真命题，并仿照他的格式写出其它真命题（无需证明）：
    真命题1：四边形ABCD中，若∠BAD=∠BCD，∠ABC=∠ADC，则四边形ABCD是平行四边形．
    （4）小亮认为，还存在一些假命题，他写出了其中的1个，并举反例进行了说明，请你仿照小亮的格式写出其它假命题并举反例进行说明．
    假命题1：四边形ABCD中，若AB=CD，AD∥BC，则四边形ABCD不一定是平行四边形．
    反例说明：如图2，四边形ABCD中，AB=CD，AD∥BC，显然四边形ABCD不是平行四边形．

    查看答案和解析>>

    同步练习册答案