
 如图,在矩形ABCD中,AB=8,BC=16,将矩形ABCD沿EF折叠,使点C与点A重合,则折痕EF的长为4$\sqrt{5}$.
如图,在矩形ABCD中,AB=8,BC=16,将矩形ABCD沿EF折叠,使点C与点A重合,则折痕EF的长为4$\sqrt{5}$. 分析 设BE=x,表示出CE=16-x,根据翻折的性质可得AE=CE,然后在Rt△ABE中,利用勾股定理列出方程求出x,再根据翻折的性质可得∠AEF=∠CEF,根据两直线平行,内错角相等可得∠AFE=∠CEF,然后求出∠AEF=∠AFE,根据等角对等边可得AE=AF,过点E作EH⊥AD于H,可得四边形ABEH是矩形,根据矩形的性质求出EH、AH,然后求出FH,再利用勾股定理列式计算即可得解.
解答 解:设BE=x,则CE=BC-BE=16-x,
∵沿EF翻折后点C与点A重合,
∴AE=CE=16-x,
在Rt△ABE中,AB2+BE2=AE2,
即82+x2=(16-x)2,
解得x=6,
∴AE=16-6=10,
由翻折的性质得,∠AEF=∠CEF,
∵矩形ABCD的对边AD∥BC,
∴∠AFE=∠CEF,
∴∠AEF=∠AFE,
∴AE=AF=10,
过点E作EH⊥AD于H,则四边形ABEH是矩形,
∴EH=AB=8,
AH=BE=6,
∴FH=AF-AH=10-6=4,
在Rt△EFH中,EF=$\sqrt{E{H}^{2}+F{H}^{2}}$=$\sqrt{{8}^{2}+{4}^{2}}$=4$\sqrt{5}$.
故答案为:4$\sqrt{5}$.
点评 本题考查了翻折变换的性质,矩形的判定与性质,勾股定理,熟记各性质并作利用勾股定理列方程求出BE的长度是解题的关键,也是本题的突破口.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:选择题
 如图,是某副食品公司销售糖果的总利润y(元)与销售量x(千克)之间的函数图象(总利润=总销售额-总成本),该公司想通过“不改变总成本,提高糖果售价”的方案解决销售不佳的现状,下面给出的四个图象,虚线均表示新的销售方案中总利润与销售量之间的函数图象,则能反映该公司改进方案的是( )
如图,是某副食品公司销售糖果的总利润y(元)与销售量x(千克)之间的函数图象(总利润=总销售额-总成本),该公司想通过“不改变总成本,提高糖果售价”的方案解决销售不佳的现状,下面给出的四个图象,虚线均表示新的销售方案中总利润与销售量之间的函数图象,则能反映该公司改进方案的是( )| A. | 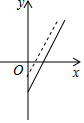 | B. |  | C. |  | D. | 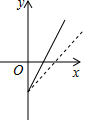 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在直角坐标系中,点P的坐标是(n,0)(n>0),抛物线y=-x2+bx+c经过原点O和点P,已知正方形ABCD的三个顶点为A(2,2),B(3,2),D(2,3).
如图,在直角坐标系中,点P的坐标是(n,0)(n>0),抛物线y=-x2+bx+c经过原点O和点P,已知正方形ABCD的三个顶点为A(2,2),B(3,2),D(2,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com