
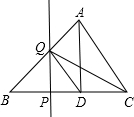
 如图,△ABC中,AD⊥BC,垂足为D,AD=BD=3,CD=2,点P从点B出发沿线段BC的方向移动到点C停止,过点P作PQ⊥BC,交折线BA-AC于点Q,连接DQ、CQ,若△ADQ与△CDQ的面积相等,则线段BP的长度是( )
如图,△ABC中,AD⊥BC,垂足为D,AD=BD=3,CD=2,点P从点B出发沿线段BC的方向移动到点C停止,过点P作PQ⊥BC,交折线BA-AC于点Q,连接DQ、CQ,若△ADQ与△CDQ的面积相等,则线段BP的长度是( )| A. | $\frac{9}{5}$或4 | B. | $\frac{6}{5}$或4 | C. | $\frac{9}{5}$或$\frac{13}{5}$ | D. | $\frac{6}{5}$或$\frac{13}{5}$ |
分析 分两种情况计算:①点Q在AB边上时,先求出三角形ABD的面积,设出BP=x,再将三角形DCQ和AQD的面积用x表示出来,用面积相等建立方程即可;②当点Q在AC边时,由面积相等即可得出点Q是AC中点,进而得出点P'是CD的中点,即可求出DP',即可得出结论.
解答 解:①点Q在AB边上时,
∵AD⊥BC,垂足为D,AD=BD=3,CD=2,
∴S△ABD=$\frac{1}{2}$BD•AD=$\frac{1}{2}$×3×3=$\frac{9}{2}$,∠B=45°
∵PQ⊥BC,
∴BP=PQ,
设BP=x,则PQ=x,
∵CD=2,
∴S△DCQ=$\frac{1}{2}$×2x=x,
S△AQD=S△ABD-S△BQD=$\frac{9}{2}$-$\frac{1}{2}$×3×x=$\frac{9}{2}$-$\frac{3}{2}$x,
∵△ADQ与△CDQ的面积相等,
∴x=$\frac{9}{2}$-$\frac{3}{2}$x,
解得:x=$\frac{9}{5}$,
②如图,
当Q在AC上时,记为Q',过点Q'作Q'P'⊥BC,
∵AD⊥BC,垂足为D,
∴Q'P'∥AD
∵△ADQ与△CDQ的面积相等,
∴AQ'=CQ'
∴DP'=CP'=$\frac{1}{2}$CD=1
∵AD=BD=3,
∴BP'=BD+DP'=4,
综上所述,线段BP的长度是$\frac{9}{5}$或4.
故选A,
点评 此题是三角形的面积,主要考查了三角形的中线将三角形分成面积相等的两个三角形,三角形的面积公式,解本题的关键是判断出点Q'是AC的中点.


科目:初中数学 来源: 题型:填空题
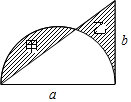 如图,已知直角三角形的两条直角边分别为a、b,以a为直径画一个半圆.若甲、乙两阴影部分的面积相等,则用a的代数式表示b=$\frac{1}{4}$πa.
如图,已知直角三角形的两条直角边分别为a、b,以a为直径画一个半圆.若甲、乙两阴影部分的面积相等,则用a的代数式表示b=$\frac{1}{4}$πa.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x(x+1)=64 | B. | x(x-1)=64 | C. | (1+x)2=64 | D. | (1+2x)=64 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
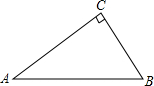 如图,某市把一块形状为直角三角形的废地开辟为生物园,∠ACB=90°,AC=80m,BC=60m.
如图,某市把一块形状为直角三角形的废地开辟为生物园,∠ACB=90°,AC=80m,BC=60m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
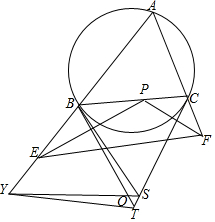 如图,在△ABC中,∠A=60°,P为线段BC(不含端点)上一点,E、F分别为射线AB、AC上的点,且BP=BE,CP=CF,△ABC的外接圆在B、C两点处的切线交于点S.设△EPF的外心为O,BO与CS交于点T,SO与直线AB交于点Y.求证:B、Y、T、S四点共圆.
如图,在△ABC中,∠A=60°,P为线段BC(不含端点)上一点,E、F分别为射线AB、AC上的点,且BP=BE,CP=CF,△ABC的外接圆在B、C两点处的切线交于点S.设△EPF的外心为O,BO与CS交于点T,SO与直线AB交于点Y.求证:B、Y、T、S四点共圆.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 近似数3.20和近似数3.2都精确到十分位 | |
| B. | 近似数3.20×103和近似数3.2×103都精确到百位 | |
| C. | 近似数2千万和近似数2000万都精确到千万位 | |
| D. | 近似数32.0和近似数3.2都精确到十分位 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com