
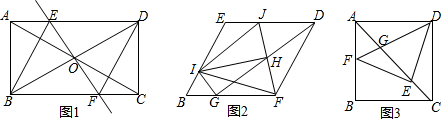
分析 (1)①由△DOE≌△BOF,推出EO=OF,∵OB=OD,推出四边形EBFD是平行四边形,再证明EB=ED即可.
②先证明∠ABD=2∠ADB,推出∠ADB=30°,延长即可解决问题.
(2)IH=$\sqrt{3}$FH.只要证明△IJF是等边三角形即可.
(3)结论:EG2=AG2+CE2.如图3中,将△ADG绕点D逆时针旋转90°得到△DCM,先证明△DEG≌△DEM,再证明△ECM是直角三角形即可解决问题.
解答 (1)①证明:如图1中,
∵四边形ABCD是矩形,
∴AD∥BC,OB=OD,
∴∠EDO=∠FBO,
在△DOE和△BOF中,
$\left\{\begin{array}{l}{∠EDO=∠FBO}\\{OD=OB}\\{∠EOD=∠BOF}\end{array}\right.$,
∴△DOE≌△BOF,
∴EO=OF,∵OB=OD,
∴四边形EBFD是平行四边形,
∵EF⊥BD,OB=OD,
∴EB=ED,
∴四边形EBFD是菱形.
②∵BE平分∠ABD,
∴∠ABE=∠EBD,
∵EB=ED,
∴∠EBD=∠EDB,
∴∠ABD=2∠ADB,
∵∠ABD+∠ADB=90°,
∴∠ADB=30°,∠ABD=60°,
∴∠ABE=∠EBO=∠OBF=30°,
∴∠EBF=60°.
(2)结论:IH=$\sqrt{3}$FH.
理由:如图2中,延长BE到M,使得EM=EJ,连接MJ.
∵四边形EBFD是菱形,∠B=60°,
∴EB=BF=ED,DE∥BF,
∴∠JDH=∠FGH,
在△DHJ和△GHF中,
$\left\{\begin{array}{l}{∠DHG=∠GHF}\\{DH=GH}\\{∠JDH=∠FGH}\end{array}\right.$,
∴△DHJ≌△GHF,
∴DJ=FG,JH=HF,
∴EJ=BG=EM=BI,
∴BE=IM=BF,
∵∠MEJ=∠B=60°,
∴△MEJ是等边三角形,
∴MJ=EM=NI,∠M=∠B=60°
在△BIF和△MJI中,
$\left\{\begin{array}{l}{BI=MJ}\\{∠B=∠M}\\{BF=IM}\end{array}\right.$,
∴△BIF≌△MJI,
∴IJ=IF,∠BFI=∠MIJ,∵HJ=HF,
∴IH⊥JF,
∵∠BFI+∠BIF=120°,
∴∠MIJ+∠BIF=120°,
∴∠JIF=60°,
∴△JIF是等边三角形,
在Rt△IHF中,∵∠IHF=90°,∠IFH=60°,
∴∠FIH=30°,
∴IH=$\sqrt{3}$FH.
(3)结论:EG2=AG2+CE2.
理由:如图3中,将△ADG绕点D逆时针旋转90°得到△DCM,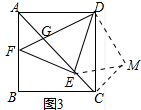
∵∠FAD+∠DEF=90°,
∴AFED四点共圆,
∴∠EDF=∠DAE=45°,∠ADC=90°,
∴∠ADF+∠EDC=45°,
∵∠ADF=∠CDM,
∴∠CDM+∠CDE=45°=∠EDG,
在△DEM和△DEG中,
$\left\{\begin{array}{l}{DE=DE}\\{∠EDG=∠EDM}\\{DG=DM}\end{array}\right.$,
∴△DEG≌△DEM,
∴GE=EM,
∵∠DCM=∠DAG=∠ACD=45°,AG=CM,
∴∠ECM=90°
∴EC2+CM2=EM2,
∵EG=EM,AG=CM,
∴GE2=AG2+CE2.
点评 本题考查四边形综合题、矩形的性质、正方形的性质、菱形的判定和性质,等边三角形的判定和性质,勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形,学会转化的思想思考问题,属于中考压轴题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | m>-3 | B. | m≥-3 | C. | m>-3且m≠$\frac{1}{2}$ | D. | m≥-3且m≠$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,己知直线AB为函数y=2x+6的图象.
如图,己知直线AB为函数y=2x+6的图象.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
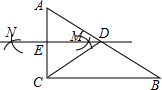 如图,在△ABC中,∠ACB=90°,分别以点A和点C为圆心,以相同的长(大于$\frac{1}{2}$AC)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交AC于点E,连接CD.下列结论错误的是( )
如图,在△ABC中,∠ACB=90°,分别以点A和点C为圆心,以相同的长(大于$\frac{1}{2}$AC)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交AC于点E,连接CD.下列结论错误的是( )| A. | AD=CD | B. | ∠A=∠DCE | C. | ∠ADE=∠DCB | D. | ∠A=2∠DCB |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1m | B. | 1.6m | C. | 1.8m | D. | 3m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com