
”¾ĢāÄæ”æøų³öČēĻĀ¹ę¶Ø£ŗ¶ŌÓŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠµÄĶ¼ŠĪM£¬N£¬øų³öČēĻĀ¶ØŅå£ŗPĪŖĶ¼ŠĪMÉĻČĪŅāŅ»µć£¬QĪŖNÉĻČĪŅ»µć£¬Čē¹ūP£¬QĮ½µć¼äµÄ¾ąĄė“ęŌŚ×īŠ”ÖµŹ±£¬¾Ķ³ĘøĆ×īŠ”ÖµĪŖĮ½øöĶ¼ŠĪMŗĶNÖ®¼äµÄ”°±Õ¾ąĄė”±£»Čē¹ūP£¬QĮ½µć¼äµÄ¾ąĄė“ęŌŚ×ī“óÖµŹ±£¬¾Ķ³ĘøĆ×ī“óÖµĪŖĮ½øöĶ¼ŠĪMŗĶNÖ®¼äµÄ”°æŖ¾ąĄė”±£®
ĒėÄćŌŚŃ§Ļ°£¬Ąķ½āÉĻŹö¶ØŅåµÄ»ł“”ÉĻ£¬½ā¾öĻĀĆęĪŹĢā£ŗ
ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬µćA£Ø©6£¬8£©£¬B£Ø©6£¬©8£©£¬C£Ø6£¬©8£©£¬D£Ø6£¬8£©£®
£Ø1£©ĒėŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ»³öĖıߊĪABCD£¬Ļ߶ĪABŗĶĻ߶ĪCDµÄ”°±Õ¾ąĄė”±ĪŖ”” ””£»”°æŖ¾ąĄė”±ĪŖ”” ””£»
£Ø2£©ÉčÖ±Ļßy£½©![]() x+b£Øb£¾0£©ÓėxÖį£¬yÖį·Ö±š½»ÓŚµćE£¬F£¬ČōĻ߶ĪEFÓėĖıߊĪABCDµÄ”°±Õ¾ąĄė”±ŹĒ2£¬ĒóĖüĆĒµÄ”°æŖ¾ąĄė”±£»
x+b£Øb£¾0£©ÓėxÖį£¬yÖį·Ö±š½»ÓŚµćE£¬F£¬ČōĻ߶ĪEFÓėĖıߊĪABCDµÄ”°±Õ¾ąĄė”±ŹĒ2£¬ĒóĖüĆĒµÄ”°æŖ¾ąĄė”±£»
£Ø3£©”ŃMµÄŌ²ŠÄĪŖM£Øm£¬©6£©£¬°ė¾¶ĪŖ1£¬Čō”ŃMÓė”÷ABCµÄ”°±Õ¾ąĄė”±µČÓŚ1£¬Ö±½ÓŠ“³ömµÄȔֵ·¶Ī§£®
”¾“š°ø”æ£Ø1£©12£¬20£»£Ø2£©2![]() »ņ2
»ņ2![]() »ņ2
»ņ2![]() £»£Ø3£©µ±m£½©8»ņ6+
£»£Ø3£©µ±m£½©8»ņ6+![]() »ņ©4”Üm”Ü6©3
»ņ©4”Üm”Ü6©3![]() Ź±£¬”ŃMÓė”÷ABCµÄ”°±Õ¾ąĄė”±µČÓŚ1£®
Ź±£¬”ŃMÓė”÷ABCµÄ”°±Õ¾ąĄė”±µČÓŚ1£®
”¾½āĪö”æ
£Ø1£©ÓɵćµÄ×ų±ź»³öĶ¼ŠĪ£¬ÓÉ”°±Õ¾ąĄė”±ŗĶ”°æŖ¾ąĄė”±µÄ¶ØŅåæÉĒó½ā£»
£Ø2£©·ÖĖÄÖÖĒéæöĢÖĀŪ£¬Ēó³öµćE£¬µćF×ų±ź£¬¼“æɽā£»
£Ø3£©·ÖµćMŌŚyÖį×ó²ąŗĶÓŅ²ąĢÖĀŪ£¬ÕŅµ½ĢŲŹāµć£¬¼“æÉĒó½ā£®
½ā£ŗ£Ø1£©ČēĶ¼ĖłŹ¾£ŗ

”ąĻ߶ĪABŗĶĻ߶ĪCDµÄ”°±Õ¾ąĄė”±ĪŖ12£¬”°æŖ¾ąĄė”±£½![]() £¬
£¬
¹Ź“š°øĪŖ£ŗ12£¬20£»
£Ø2£©”ßĻ߶ĪEFÓėĖıߊĪABCDµÄ”°±Õ¾ąĄė”±ŹĒ2£¬
”ąµćE×ų±źĪŖ£Ø4£¬0£©»ņµćE£Ø8£¬0£©»ņµćF£Ø0£¬6£©»ņµćF£Ø0£¬10£©
µ±µćE×ų±źĪŖ£Ø4£¬0£©Ź±£¬
”ą0£½©![]() ”Į4+b£¬
”Į4+b£¬
”ąb£½3£¬
”ąµćF£Ø0£¬3£©£¬
”ąĻ߶ĪEFÓėĖıߊĪABCDµÄ”°æŖ¾ąĄė”±£½![]() £¬
£¬
µ±µćE×ų±źĪŖ£Ø8£¬0£©Ź±£¬
”ą0£½©![]() ”Į8+b£¬
”Į8+b£¬
”ąb£½6£¬
”ąµćF£Ø0£¬6£©£¬
”ąĻ߶ĪEFÓėĖıߊĪABCDµÄ”°æŖ¾ąĄė”±£½![]() £¬
£¬
µ±µćF×ų±źĪŖ£Ø0£¬6£©Ź±£¬
”ąb£½6£¬
”ąy£½©![]() x+6£¬
x+6£¬
”ąµćE£Ø8£¬0£©£¬
”ąĻ߶ĪEFÓėĖıߊĪABCDµÄ”°æŖ¾ąĄė”±£½![]() £¬
£¬
µ±µćF×ų±źĪŖ£Ø0£¬10£©Ź±£¬
”ąb£½10£¬
”ąy£½©![]() x+10£¬
x+10£¬
”ąµćE£Ø![]() £¬0£©
£¬0£©
”ąĻ߶ĪEFÓėĖıߊĪABCDµÄ”°æŖ¾ąĄė”±£½![]() £¬
£¬
£Ø3£©ČēĶ¼£¬ÉčÖ±Ļßy£½©6ÓėAB½»ÓŚµćN£¬½»ACÓŚµćE£¬

”ßM£Øm£¬©6£©£¬°ė¾¶ĪŖ1£¬
”ąµ±µćMŌŚyÖį×ó²ąŹ±£¬MN£½2Ź±£¬”ŃMÓė”÷ABCµÄ”°±Õ¾ąĄė”±µČÓŚ1£¬
”ąm£½©8»ņ©4£¬
µ±µćMŌŚyÖįÓŅ²ąŹ±£¬ME£½2![]() Ź±£¬”ŃMÓė”÷ABCµÄ”°±Õ¾ąĄė”±µČÓŚ1£¬
Ź±£¬”ŃMÓė”÷ABCµÄ”°±Õ¾ąĄė”±µČÓŚ1£¬
”ąm£½6+![]() »ņ6©3
»ņ6©3![]() £¬
£¬
”ąµ±m£½©8»ņ6+![]() »ņ©4”Üm”Ü6©3
»ņ©4”Üm”Ü6©3![]() Ź±£¬”ŃMÓė”÷ABCµÄ”°±Õ¾ąĄė”±µČÓŚ1£®
Ź±£¬”ŃMÓė”÷ABCµÄ”°±Õ¾ąĄė”±µČÓŚ1£®


 ĆūŠ£æĪĢĆĻµĮŠ“š°ø
ĆūŠ£æĪĢĆĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚ¾ŲŠĪABCDÖŠ£¬AB£½5 cm£¬BC£½6 cm£¬µćP“ÓµćAæŖŹ¼ŃŲABĻņÖÕµćBŅŌ1 cm/sµÄĖŁ¶ČŅĘ¶Æ£¬Óė“ĖĶ¬Ź±£¬µćQ“ÓµćBæŖŹ¼ŃŲ±ßBCĻņÖÕµćCŅŌ2 cm/sµÄĖŁ¶ČŅĘ¶Æ£¬Čē¹ūP”¢Q·Ö±š“ÓA”¢BĶ¬Ź±³ö·¢£¬µ±µćQŌĖ¶Æµ½µćCŹ±£¬Į½µćĶ£Ö¹ŌĖ¶Æ£¬ÉčŌĖ¶ÆŹ±¼äĪŖtĆė£®
(1)ĢīæÕ£ŗBQ£½________£¬PB£½________(ÓĆŗ¬tµÄ“śŹżŹ½±ķŹ¾)£»
(2)µ±tĪŖŗĪÖµŹ±£¬PQµÄ³¤¶ČµČÓŚ![]() cm?
cm?
(3)ŹĒ·ń“ęŌŚtµÄÖµ£¬Ź¹µĆĪå±ßŠĪAPQCDµÄĆ껿µČÓŚ26 cm2£æČō“ęŌŚ£¬ĒėĒó³ö“ĖŹ±tµÄÖµ£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Å×ĪļĻßy=©![]() x2+bx+cÓėxÖį½»ÓŚµćA£¬B£¬ÓėyÖį½»ÓŚµćC£¬Ö±Ļßy=x+4¾¹żA£¬CĮ½µć£®
x2+bx+cÓėxÖį½»ÓŚµćA£¬B£¬ÓėyÖį½»ÓŚµćC£¬Ö±Ļßy=x+4¾¹żA£¬CĮ½µć£®

£Ø1£©ĒóÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©ŌŚACÉĻ·½µÄÅ×ĪļĻßÉĻÓŠŅ»¶ÆµćP£®
¢ŁČēĶ¼1£¬µ±µćPŌĖ¶Æµ½Ä³Ī»ÖĆŹ±£¬ŅŌAP£¬AOĪŖĮŚ±ßµÄĘ½ŠŠĖıߊĪµŚĖÄøö¶„µćĒ”ŗĆŅ²ŌŚÅ×ĪļĻßÉĻ£¬Ēó³ö“ĖŹ±µćPµÄ×ų±ź£»
¢ŚČēĶ¼2£¬¹żµćO£¬PµÄÖ±Ļßy=kx½»ACÓŚµćE£¬ČōPE£ŗOE=3£ŗ8£¬ĒókµÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æij»¬Ń©³”¾Ł°ģ±łŃ©¼ĪÄź»Ŗ»ī¶Æ£¬²ÉÓĆֱɿ»śŗ½Åļ¼ŹõÅÄÉć»ī¶ÆŹ¢æö£¬ČēĶ¼£¬ĶعżÖ±Éż»śµÄ¾µĶ·C¹Ū²āµ½Ė®Ę½Ń©µĄŅ»¶ĖA“¦µÄø©½ĒĪŖ30”ć£¬ĮķŅ»¶ĖB“¦µÄø©½ĒĪŖ45”ć£®Čōֱɿ»ś¾µĶ·C“¦µÄø߶ČCDĪŖ200Ć×£¬µćA”¢D”¢BŌŚĶ¬Ņ»Ö±ĻßÉĻ£¬ŌņŃ©µĄABµÄ³¤¶ČĪŖ£Ø””””£©

A.200 Ć×B.£Ø200+200![]() £©Ć×
£©Ć×
C.600 Ć×D.£Ø200+20![]() £©Ć×
£©Ć×
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ABŹĒ”ŃOµÄÖ±¾¶£¬BC½»”ŃOÓŚµćD£¬EŹĒ![]() µÄÖŠµć£¬Į¬½ÓAE½»BCÓŚµćF£¬”ĻACB=2”ĻEAB£®
µÄÖŠµć£¬Į¬½ÓAE½»BCÓŚµćF£¬”ĻACB=2”ĻEAB£®

£Ø1£©ĒóÖ¤£ŗACŹĒ”ŃOµÄĒŠĻߣ»
£Ø2£©ČōcosC=![]() £¬AC=6£¬ĒóBFµÄ³¤£®
£¬AC=6£¬ĒóBFµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ Ä³Ń§Š£ĪŖĮĖĮĖ½ā°ĖÄź¼¶Ń§ÉśµÄæĪĶāŌĶĮĒéæö£¬Ė껜³é²é²æ·Öѧɜ£¬²¢¶ŌĘä4ŌĀ·ŻµÄæĪĶāŌĶĮĮæ½ųŠŠĶ³¼Ę·ÖĪö£¬»ęÖĘ³ÉČēĶ¼ĖłŹ¾µÄĶ³¼ĘĶ¼£ØŹż¾Ż²»ĶźÕū£©£®
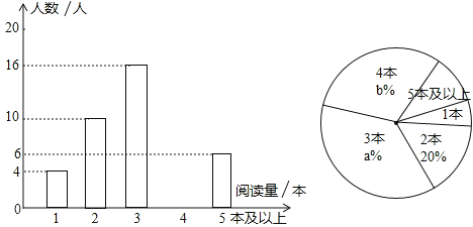
øł¾ŻĶ¼Ź¾ŠÅĻ¢£¬½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©±¾“Ī±»³é²éµÄѧɜ¹²ÓŠ______ČĖ£»
£Ø2£©a=______£¬b=______£¬½«ĢõŠĪĶ³¼ĘĶ¼²¹³äĶźÕū£»
£Ø3£©æĪĶāŌĶĮĮæµÄÖŚŹżŹĒ______±¾£»
£Ø4£©Čō¹ę¶Ø£ŗ4ŌĀ·ŻŌĶĮ3±¾ŅŌÉĻ£Øŗ¬3±¾£©æĪĶāŹé¼®ÕßĪŖĶź³ÉŌĶĮČĪĪń£¬¾Ż“Ė¹Ą¼ĘøĆŠ£°ĖÄź¼¶800Ćūѧɜ֊£¬Ķź³É4ŌĀ·ŻæĪĶāŌĶĮČĪĪńµÄŌ¼ÓŠ¶ąÉŁČĖ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻĀĮŠĆüĢāÕżČ·µÄŹĒ£Ø””””£©
A.øÅĀŹŹĒ1%µÄŹĀ¼žŌŚŅ»“ĪŹŌŃéÖŠŅ»¶Ø²»»į·¢Éś
B.ŅŖĮĖ½āij¹«Ė¾Éś²śµÄ100ĶņÖ»µĘÅŻµÄŹ¹ÓĆŹŁĆü£¬æÉŅŌ²ÉÓĆČ«Ćęµ÷²éµÄ·½Ź½
C.¼×ŅŅĮ½ČĖø÷×ŌĢųŌ¶10“Ī£¬ČōĖūĆĒĢųŌ¶³É¼ØµÄĘ½¾łŹżĻąĶ¬£¬¼×ŅŅĢųŌ¶³É¼ØµÄ·½²ī·Ö±šĪŖ0.51ŗĶ0.62£¬ŌņŅŅµÄ³É¼ØøüĪȶØ
D.ĖęŅā·µ½Ņ»±¾ŹéµÄijŅ³£¬Ņ³ĀėŹĒĘꏿŹĒĖ껜ŹĀ¼ž
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ4ŌĀ23ČÕŹĒ”°ŹĄ½ēĶ¼ŹéÓė°ęČØČÕ”±£Ø¼ņ³Ę”°ŹĄ½ē¶ĮŹéČÕ”±£©£¬ÉčĮ¢ÄæµÄŹĒĶʶÆøü¶ąµÄČĖŌĶĮŗĶŠ“×÷£¬ÄĻæŖ¶ĮŹéÉē¶Ō³õČżÄ³°ą½ųŠŠĮĖ”°Äć×īĻ²»¶µÄŹé¼®Ąą±š”±µÄĪŹ¾ķµ÷²é£®ÓĆ”°![]() ”±±ķŹ¾Š”ĖµĄąŹé¼®£¬”°
”±±ķŹ¾Š”ĖµĄąŹé¼®£¬”°![]() ”±±ķŹ¾ĪÄѧĄąŹé¼®£¬”°
”±±ķŹ¾ĪÄѧĄąŹé¼®£¬”°![]() ”±±ķŹ¾“«¼ĒĄąŹé¼®£¬”°
”±±ķŹ¾“«¼ĒĄąŹé¼®£¬”°![]() ”±±ķŹ¾ŅÕŹõĄąŹé¼®£®øł¾ŻĪŹ¾ķµ÷²éĶ³¼Ę׏ĮĻ»ęÖĘĮĖČēĻĀĮ½·ł²»ĶźÕūµÄĶ³¼ĘĶ¼£¬ĒėÄćøł¾ŻĶ³¼ĘĶ¼Ģį¹©µÄŠÅĻ¢½ā“šŅŌĻĀĪŹĢā£ŗ
”±±ķŹ¾ŅÕŹõĄąŹé¼®£®øł¾ŻĪŹ¾ķµ÷²éĶ³¼Ę׏ĮĻ»ęÖĘĮĖČēĻĀĮ½·ł²»ĶźÕūµÄĶ³¼ĘĶ¼£¬ĒėÄćøł¾ŻĶ³¼ĘĶ¼Ģį¹©µÄŠÅĻ¢½ā“šŅŌĻĀĪŹĢā£ŗ
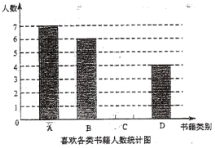
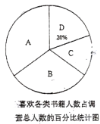
£Ø1£©±¾“ĪĪŹ¾ķµ÷²é£¬¹²µ÷²éĮĖ Ćūѧɜ£¬Ēė²¹Č«ĻĀĮŠĢõŠĪĶ³¼ĘĶ¼ŗĶÉČŠĪĶ³¼ĘĶ¼£»
£Ø2£©ŌŚ½ÓŹÜĪŹ¾ķµ÷²éµÄѧɜ֊£¬Ļ²»¶”°![]() ”±µÄČĖÖŠÓŠ2ĆūŹĒÄŠÉś£¬Ļ²»¶”°
”±µÄČĖÖŠÓŠ2ĆūŹĒÄŠÉś£¬Ļ²»¶”°![]() ”±µÄČĖÖŠÓŠ1ĆūŹĒÄŠÉś£¬ĻÖ·Ö±š“ÓĻ²»¶ÕāĮ½ĄąŹé¼®Ń§ÉśÖŠø÷½ųŠŠ¶ĮŹéŠÄµĆ½»Į÷£¬ĒėÓĆ»Ź÷דĶ¼»ņĮŠ±ķ·ØĒó³öøÕŗĆє֊2Ćū¶¼ŹĒÄŠÉśµÄøÅĀŹ£®
”±µÄČĖÖŠÓŠ1ĆūŹĒÄŠÉś£¬ĻÖ·Ö±š“ÓĻ²»¶ÕāĮ½ĄąŹé¼®Ń§ÉśÖŠø÷½ųŠŠ¶ĮŹéŠÄµĆ½»Į÷£¬ĒėÓĆ»Ź÷דĶ¼»ņĮŠ±ķ·ØĒó³öøÕŗĆє֊2Ćū¶¼ŹĒÄŠÉśµÄøÅĀŹ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ¶ž“ĪŗÆŹż![]() £Ø
£Ø![]() £©µÄĶ¼ĻóÓė
£©µÄĶ¼ĻóÓė![]() Öį½»ÓŚ²»Ķ¬µÄĮ½µć
Öį½»ÓŚ²»Ķ¬µÄĮ½µć![]() £¬
£¬![]() ĪŖ¶ž“ĪŗÆŹżĶ¼ĻóµÄ¶„µć£®Čō
ĪŖ¶ž“ĪŗÆŹżĶ¼ĻóµÄ¶„µć£®Čō![]() ŹĒ±ß³¤ĪŖ4µÄµČ±ßČż½ĒŠĪ£¬Ōņ
ŹĒ±ß³¤ĪŖ4µÄµČ±ßČż½ĒŠĪ£¬Ōņ![]() __________£®
__________£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com