
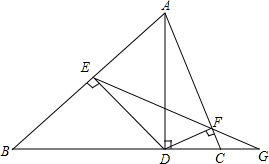
 已知AD是△ABC的高,点D在BC内,且BD=3,CD=1,作DE⊥AB于点E,DF⊥AC于点F,连接EF并延长,交BC的延长线于点G,求CG.
已知AD是△ABC的高,点D在BC内,且BD=3,CD=1,作DE⊥AB于点E,DF⊥AC于点F,连接EF并延长,交BC的延长线于点G,求CG. 分析 首先根据∠AED+∠AFD=90°+90°=180°得到A,E,D,F四点共圆,然后根据圆的性质得到∠GFC=∠AFE=∠ADE=∠B,∠FDC=∠DAF=∠DEF,从而得到△GFC∽△GBE,△GFD∽△GDE,利用相似三角形的性质得到(CG+1)(CG+1)=CG•(CG+4),从而求得CG的长.
解答 解:∵∠AED+∠AFD=90°+90°=180°,
∴A,E,D,F四点共圆,
∴∠GFC=∠AFE=∠ADE=∠B,∠FDC=∠DAF=∠DEF,
∴△GFC∽△GBE,△GFD∽△GDE,
∴FG•GE=CG•GB,GF•GE=DG•DG,
∴DG•DG=CG•GB,
即(CG+1)(CG+1)=CG•(CG+4),
解得:CG=0.5.
点评 本题考查了相似三角形的判定与性质及四点共圆的知识,解题的关键是能够根据两个直角确定四点共圆,难点中等偏上.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
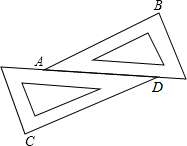 用两块相同的三角板按如图所示的方式作平行线AB和CD,能解释其中的道理的依据是( )
用两块相同的三角板按如图所示的方式作平行线AB和CD,能解释其中的道理的依据是( )| A. | 内错角相等,两直线平行 | B. | 同位角相等,两直线平行 | ||
| C. | 同旁内角互补,两直线平行 | D. | 平行于同一直线的两直线平行 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ① | B. | ①④ | C. | ①③ | D. | ①②④⑥ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB于点E,则tan∠BDE的值等于( )
如图,在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB于点E,则tan∠BDE的值等于( )| A. | $\frac{10}{13}$ | B. | $\frac{13}{10}$ | C. | $\frac{5}{12}$ | D. | $\frac{12}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com