(1)阅读下面材料:
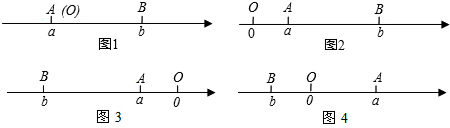
点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为∣AB∣。当A、B两点中有一点在原点时,不妨设点A在原点,如图1,∣AB∣=∣OB∣=∣b∣=∣a-b∣;当A、B两点都不在原点时,如图2,点A、B都在原点的右边∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=b-a=∣a-b∣;
① 如图3,点A、B都在原点的左边,∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=-b-(-a)=∣a-b∣;
② 如图4,点A、B在原点的两边,∣AB∣=∣OB∣+∣OA∣=∣a∣+∣b∣=" a" +(-b)=∣a-b∣;
(2)回答下列问题:
【小题1】数轴上表示2和5的两点之间的距离是_________,数轴上表示-2和-5的两点之间的距离是_________,数轴上表示1和-3的两点之间的距离是_______;(共3分)
【小题2】数轴上表示x和-1的两点A和B之间的距离是_____,如果∣AB∣=2,那么x为_
___ (共4分)
【小题3】当代数式∣x+1∣+∣x-2∣+∣x+3∣取最小值时,相应的x的值是___________;此时代数式∣x+1∣+∣x-2∣+∣x+3∣的值是_____________.(6分)


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案