
分析 ①④⑤⑥根据有理数的混合运算的运算方法,求出每个算式的值各是多少即可.
②应用加法交换律和加法结合律,求出算式的值是多少即可.
③应用乘法分配律,求出每个算式的值各是多少即可.
解答 解:①(-30)-(-28)+(-70)-88
=-2-70-88
=-160
②2$\frac{2}{3}$+(-2$\frac{1}{2}$)+5$\frac{1}{3}$+(-5$\frac{1}{2}$)
=(2$\frac{2}{3}$+5$\frac{1}{3}$)-(2$\frac{1}{2}$+5$\frac{1}{2}$)
=8-8
=0
③($\frac{1}{3}$-$\frac{3}{14}$-1$\frac{2}{7}$)×(-42)
=$\frac{1}{3}$×(-42)-$\frac{3}{14}$×(-42)-1$\frac{2}{7}$×(-42)
=-14+9+54
=49
④$\frac{7}{5}$×($\frac{1}{3}$-$\frac{1}{2}$)×$\frac{3}{7}$÷$\frac{2}{5}$
=$\frac{7}{5}$×(-$\frac{1}{6}$)×$\frac{3}{7}$÷$\frac{2}{5}$
=(-$\frac{7}{30}$)×$\frac{3}{7}$÷$\frac{2}{5}$
=(-$\frac{1}{10}$)÷$\frac{2}{5}$
=-$\frac{1}{4}$
⑤10+8×(-$\frac{1}{2}$)2-2÷$\frac{1}{5}$
=10+2-10
=12-10
=2
⑥-14-[1-(1-0.5×$\frac{1}{3}$)]×[2-(-3)2]
=-1-[1-(1-$\frac{1}{6}$)]×[2-9]
=-1-$\frac{1}{6}$×[-7]
=$\frac{1}{6}$
点评 此题主要考查了有理数的混合运算,要熟练掌握,注意明确有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -a2-b2 | B. | x2+2x+4 | C. | -(-a)2-b2 | D. | ${x^2}+x+\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
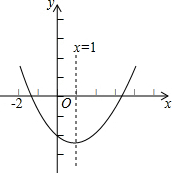 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①b2>4ac;②abc>0;③2a-b=0;④9a+3b+c<0,其中结论正确有( )个.
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①b2>4ac;②abc>0;③2a-b=0;④9a+3b+c<0,其中结论正确有( )个.| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com